Si vous souhaitez travailler en finance, que ce soit en Corporate Finance ou en finance de marché, il y a une méthode de valorisation que vous devez absolument connaître : le modèle du Discounted Cash Flow, souvent abrégé en DCF.
C’est bien simple, le Discounted Cash Flow est une méthode emblématique de la valorisation financière. C’est un concept phare que vous devez absolument connaitre sur le bout des doigts pour travailler en finance.
Le Discounted Cash Flow permet de valoriser aussi bien une entreprise dans sa totalité, qu’une action, une obligation ou tout autre produit financier ou investissement, comme de l’immobilier ou des actifs industriels.
Pas d’inquiétudes, The Big Win vous explique tout ce que vous devez savoir sur le Discounted Cash Flow de manière simple et efficace.

- Qu’est-ce que la méthode du Discounted Cash Flow : définition
- La notion d’actualisation : principe fondamental de la méthode du Discounted Cash Flow
- Formule pour une valorisation par les Discounted Cash Flow
- Cas pratique d’un calcul de Discounted Cash Flow à la main et sur Excel
- Choisir les bons cash flows dans votre calcul de DCF
- Choisir le bon taux d’actualisation
- Compléter vos valorisations par les DCF avec des multiples de valorisation
Qu’est-ce que la méthode du Discounted Cash Flow : définition
La méthode du Discounted Cash Flow (DCF) est avant tout une méthode de valorisation qui permet de calculer la valeur d’un actif au sens large : entreprise, action, obligation, dette, immobilier, actif industriel, propriété intellectuelle, etc…
Cette méthode de valorisation est construite sur un raisonnement très simple et logique : la valeur d’un investissement aujourd’hui doit être égale à la somme des revenus actualisés (discounted en anglais) que cet investissement apportera dans le futur.
Par exemple, la valeur d’un bien immobilier doit être environ égale à la somme des loyers qu’il permettra de toucher à l’avenir.
La méthode du Discounted Cash Flow a pour but d’appliquer ce raisonnement à tous les types d’investissements puisque le principe même d’un investissement est de dépenser de l’argent tout de suite pour en toucher plus dans le futur. La méthode des DCF vise donc simplement à mettre un signe “égal” entre ce coût immédiat et ces revenus futurs.
Par conséquent, la méthode des DCF est utilisée dans tous les secteurs financiers, sans exception, dès qu’il est nécessaire de valoriser un investissement ou un actif :
- En gestion action pour établir la valeur intrinsèque d’une action et comparer cette valeur à son prix sur le marché. Si le prix de l’action en bourse est inférieur à la valeur par les DCF, cela veut dire que l’action est sous-cotée et qu’elle représente donc, en théorie, un bon investissement.
- En fusion-acquisition ou en LBO pour valoriser une entreprise cible et ainsi donner une indication du prix à proposer au vendeur pour acquérir la société en vente.
- En Private Equity, à l’instar du M&A, cela permet de calculer la valorisation d’une société pour acquérir un certain pourcentage de son capital lorsqu’elle lève des fonds.
- C’est aussi une méthode de valorisation très utilisée en investissement immobilier ou infrastructure, comme lorsqu’un fond d’investissement rachète par exemple des concessions autoroutières ou un aéroport. L’objectif est ainsi d’estimer les revenus futurs de ces actifs immobiliers ou infrastructure et de proposer un prix d’acquisition inférieur ou égal à la somme des revenus futurs actualisés.
Attention cependant, nous ne pouvons pas mettre aussi facilement un signe “égal” entre le présent et le futur, surtout en finance. En effet, 1€ aujourd’hui ne vaut pas forcément 1€ demain, et 1€ demain ne vaut pas non plus 1€ après-demain. C’est cet aspect de la “valeur de l’argent dans le temps” que symbolise le “discounted” (ou “actualisé » en français) et nous vous l’expliquons dans la partie suivante de notre article.
La notion d’actualisation : principe fondamental de la méthode du Discounted Cash Flow
Avant de rentrer dans le détail de la méthode Discounted Cash Flow, il est nécessaire de s’attarder quelques instants sur son principe fondateur : la valeur de l’argent dans le temps, modélisée mathématiquement parlant par le principe d’actualisation.
Comme nous vous le disions précédemment, une même somme d’argent n’a pas la même valeur aujourd’hui, demain ou dans un an. Un adage populaire le décrit d’ailleurs très bien ce raisonnement : “un tient vaut mieux que deux tu l’auras”.
Voici quelques raisons qui explique qu’1€ aujourd’hui vaut plus qu’1€ dans un an :
- La première raison est qu’il faut prendre en compte la notion de risque, notion que nous avons aussi abordée dans notre article sur le taux sans risque. Attendre de dépenser votre euro dans un an, c’est prendre le risque de le perdre d’ici là : votre banque peut faire faillite par exemple. Pour que vous acceptiez de prendre ce risque, il vous faut une bonne raison : par exemple, le fait que votre euro d’aujourd’hui se transforme en 2€ dans un an. Là effectivement, cela vaut le coup d’attendre et de prendre des risques.
- La deuxième raison est liée à ce que l’on appelle en finance la “utility curve”. Elle représente, en quelque sorte, la satisfaction d’un investisseur. Ainsi, pourquoi attendre un an avant de dépenser votre euro pour vous acheter ce qui vous fait plaisir, alors que vous pourriez l’acheter tout de suite. Toujours pour la même raison : savoir que votre euro d’aujourd’hui vaudra deux euros dans un an.
- Une troisième raison est l’inflation. L’inflation fait qu’une somme d’argent fixe perd de la valeur dans le temps : les prix augmentent donc vous pourrez acheter moins avec votre euro dans un an que ce que vous pouvez acheter aujourd’hui. Par conséquent, il faut là encore que votre euro se transforme en 2€ pour compenser l’inflation si vous ne voulez pas perdre du pouvoir d’achat.
Tous ces facteurs font donc que la valeur d’une somme n’est pas égale dans le temps. Pour conserver une valeur égale, une somme d’argent doit augmenter dans le temps afin de compenser les mécanismes que nous venons de voir.
Ainsi pour une somme S d’argent en année (n), la fonction suivante permet d’obtenir son équivalent en année (n+1) pour conserver la même valeur :
S(n+1) = S(n) * (1 + t)
t : le taux d’actualisation.
Par exemple, pour un taux d’actualisation de 5%, 1 euro en 2020 vaut 1,05€ en 2021 et 1,1025€ en 2022, etc…
Ce calcul est strictement similaire au calcul que vous pouvez faire pour estimer la rentabilité d’un placement financier, rien de très original donc.
Cependant, là où il devient très intéressant c’est lorsqu’on se rend compte qu’il permet de relier présent et futur : c’est exactement ce que l’on veut avec la méthode du discounted cash flow, à savoir estimer une valeur actuelle de revenus futurs.
Formule pour une valorisation par les Discounted Cash Flow
Formule de Discounted Cash Flow à durée finie
Maintenant que nous avons étudié le principe d’actualisation qui sous-tend la méthode de valorisation du Discounted Cash Flow, voyons désormais sa formule exacte.
L’idée générale est donc que la valeur d’un investissement est égale à la somme de ses revenus futurs actualisés. Il nous suffit donc de faire cette somme :
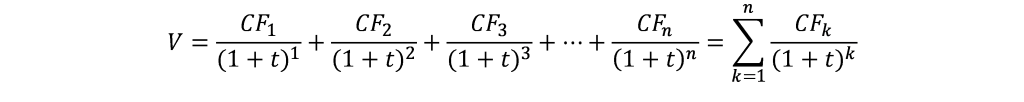
Avec :
- V = la valorisation actuelle de l’actif que nous évaluons ;
- CF = cash flow de l’année 1, 2, 3, … n ;
- t = le taux d’actualisation que nous retenons.
Ainsi, la valorisation actuelle de l’actif qui vous intéresse est égale à la somme des revenus futurs actualisés que l’investissement vous rapporte.
Comme vous l’avez peut-être remarqué, la formule de Discounted Cash Flow est la même que celle de la Valeur Actuelle Nette (VAN) aussi appelée Net Present Value (NPV) en anglais.
Nous verrons d’ailleurs un peu plus loin dans l’article comment profiter de cette similitude avec la VAN pour faire une valorisation par la méthode de Discounted Cash Flow dans Excel.
Formule de Discount Cash Flow à l’infinie : la notion de valeur terminale
Mais comment calculer la somme ci-dessus lorsque votre investissement n’a pas de durée limitée et qu’il est ainsi censé vous rapporter des cash flows “à l’infini” ? Par exemple, dans le cas d’une action ou d’un bien immobilier que vous ne souhaitez pas revendre.
Dans cette optique, la solution est de rajouter une valeur terminale à votre formule de Discounted Cash Flow, valeur que vous ajouterez comme les autres cash flows dans la formule que nous vous avons présentée.
Tout d’abord, voici la formule de la valeur terminale :

Avec :
- Vt = la valeur terminale de l’actif que vous étudiez
- CF = le cash flow que vous rapportera votre investissement “à l’infini”, par exemple, le dividende de votre action ou le loyer de votre appartement
- t = votre taux d’actualisation
- g = le taux de croissance des revenus de votre actif à l’infini si vous pensez que les revenus de votre investissement vont continuer d’augmenter “à l’infini’
Enfin, il vous suffit d’ajouter cette valeur terminale à la fin du calcul de Discounted Cash Flow que nous vous avons exposé précédemment :
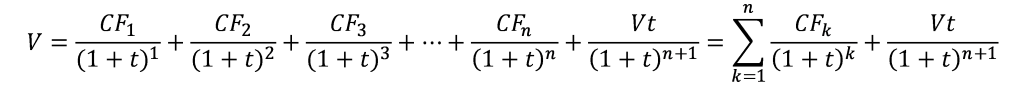
Cas pratique d’un calcul de Discounted Cash Flow à la main et sur Excel
Exemple d’un calcul de Discounted Cash Flow à la main
Maintenant que nous avons vu en quoi consistait un calcul de Discounted Cash Flow, un petit exemple s’impose pour éclaircir ces formules.
Essayons ainsi de valoriser l’action d’une entreprise fictive, BigWin Inc, cotée au NASDAQ. Comme cash flow, nous allons prendre les dividendes que cette action paye tous les ans.
Après une étude poussée de la société BigWin Inc, vous pensez que l’entreprise sera en mesure de payer les dividendes suivants au cours des 5 prochaines années :
- 2€ dans 1 an ;
- 3€ dans 2 ans ;
- 1€ dans 3 ans (l’entreprise devra faire de lourds investissements ce qui explique une baisse des dividendes) ;
- 4€ dans 4 ans ;
- 5€ dans 5 ans ;
- Vous pensez ensuite que BigWin Inc sera capable de tenir un niveau de dividende de 4€ “à l’infini”.
Vous pensez également que l’entreprise BigWin Inc va connaitre un taux de croissance de 2% par an à l’infini.
Votre taux d’actualisation est quant à lui de 5%.
Pour valoriser l’action de BigWin Inc, vous pouvez alors utiliser la méthode de Discounted Cash Flow comme nous l’avons expliquée précédemment.
Commençons par le calcul de la valeur terminale :
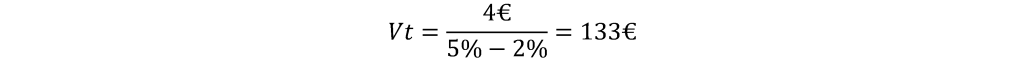
Maintenons que nous avons la valeur terminale, nous pouvons utiliser la formule de Discounted Cash Flow totale :
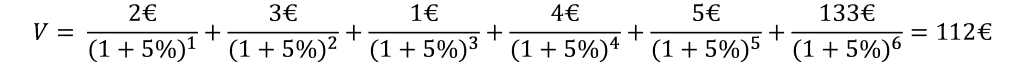
Nous déduisons donc que la valeur de l’action BigWin Inc est de 112€.
Si son prix sur le marché est inférieur à 112€, c’est donc le moment d’acheter, cela veut dire que vous pouvez l’acquérir pour moins cher que sa valeur intrinsèque et faire un joli coup !
Au contraire, si son prix est supérieur à 112€ sur le marché, cela veut dire qu’elle est surévaluée et que vous devez passer votre chemin.
Exemple d’un calcul de Discounted Cash Flow sur Excel
Maintenant que vous savez utiliser la formule de Discounted Cash Flow pour calculer la valeur d’un actif, ne nous voilons pas la face : dans le monde professionnel, personne n’utilise la formule scolaire pour faire ses petits calculs à la main.
Vous devez donc apprendre à utiliser la méthode des DCF sur Excel. Dans ce cas, sa similitude avec la VAN permet d’utiliser la fonction dédiée sur Excel pour vous faire gagner encore plus de temps.
Si nous reprenons exactement le même exemple que précédemment, avec l’entreprise BigWin Inc, voilà ce que cela donne en image :
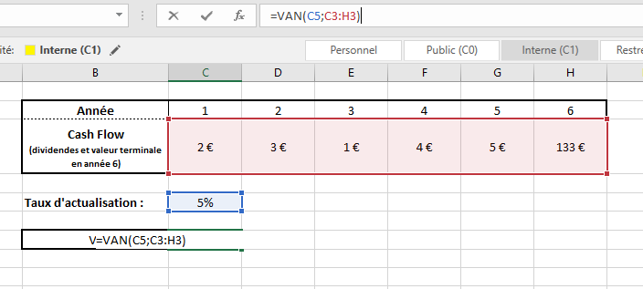
Et voici ce que cela donne avec le résultat :
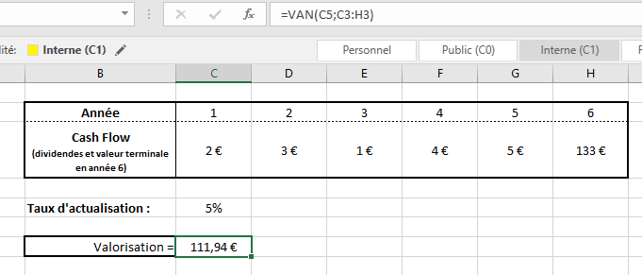
Si nous arrondissons à l’unité, nous retrouvons bien les 112€ du résultat précédent.
Mais, nous pouvons encore faire mieux, en utilisant non pas la formule VAN mais la formule VAN.PAIEMENT.
La formule VAN.PAIEMENT permet d’obtenir un résultat encore plus précis en prenant en compte les dates exactes de versement des cash flow. En effet, imaginons que les cash flows de BigWin Inc ne soient pas toujours distribués exactement à la même date et que vous-même ne fassiez pas votre calcul de valorisation pile un an avant le premier versement.
Dans ce cas, la formule VAN.PAIEMENT est beaucoup plus précise car elle actualisera chaque cash flow sur la durée exacte qu’il faut.
En reprenant notre exemple précédent, imaginons par exemple que vous fassiez votre calcul un 14 mars, et que, pour une raison inconnue, la société BigWin Inc verse ses dividendes alternativement en novembre ou en décembre chaque année.
Dans ce cas, la formule VAN.PAIEMENT prendra en compte l’aspect irrégulier des intervalles de temps dans son calcul :
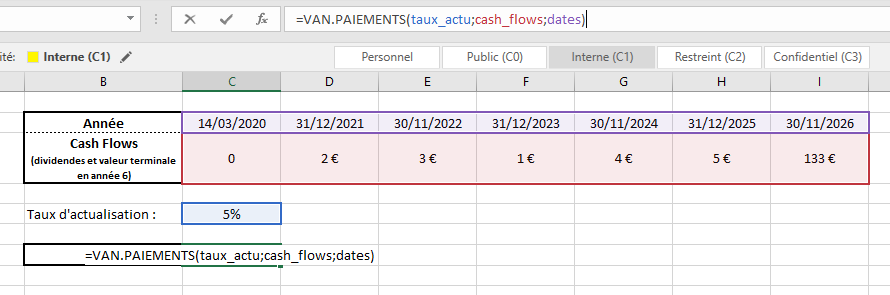
Pour le résultat suivant :
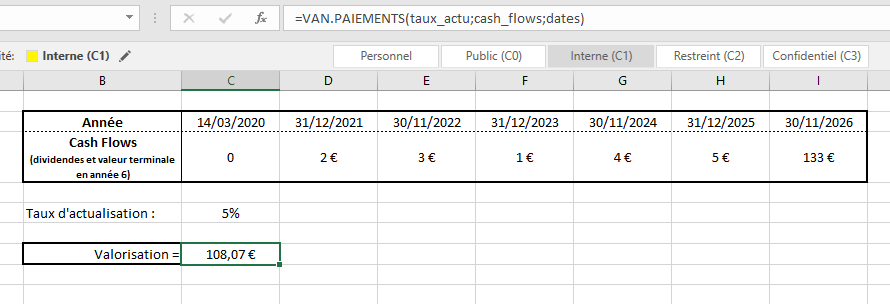
Comme vous pouvez le remarquer, le résultat est très légèrement différent du calcul en utilisant simplement la formule VAN.
De plus, vous noterez que nous mettons une colonne (en C) à la date à laquelle nous voulons notre résultat. En effet, la formule VAN.PAIEMENT donne le résultat à la première date que vous indiquez dans votre tableau. Ainsi, si nous n’avions pas mis la date du 14/03/2021, nous aurions eu une valorisation à la date du 31/12/2021 ce qui n’est pas la date que nous ciblons. Bien évidemment, nous mettons un cash flow de 0 à cette date puisqu’elle ne correspond pas à une date à laquelle nous recevons des dividendes mais à la date à laquelle nous voulons notre résultat. Faites attention à ce détail si la date à laquelle vous souhaitez votre résultat ne correspond pas à la date de votre premier cash flow.
Choisir les bons cash flows dans votre calcul de DCF
Maintenant que vous savez parfaitement utiliser la méthode de Discounted Cash Flow pour valoriser un actif, il vous reste à bien choisir… vos cash flows justement !
En effet, en fonction des cash flows que vous choisirez, vous ne valoriserez pas du tout la même chose.
Voici les principaux cash flows utilisés habituellement dans une valorisation par Discounted Cash Flow :
L’utilisation des Free Cash Flow to Firm (FCFF) dans le Discounted Cash Flow
Les Free Cash Flow to Firm (abrégés en FCFF) font partie des cash fows les plus utilisés dans un modèle de Discounted Cash Flow pour valoriser la totalité d’une entreprise, c’est à dire la valeur du capital social et la valeur des dettes.
C’est donc une métrique très utilisée en Private Equity ou en M&A.
Le Free Cash Flow to Firm est le cash flow disponible pour tous les investisseurs d’une entreprise. Autrement dit, le FCFF rémunère tous les apporteurs en fonds propres (Equity), aussi appelés actionnaires, et tous les apporteurs en dettes (Debt), aussi appelés créanciers.
Le FCFF se calcule de la manière suivante :
FCFF = EBIT * (1 – Tax) + Depreciation & Amortization – Changes in Working Capital – Capital Expenditures
Ou en français :
FCFF = EBIT * (1 – Taux d’impôts sur les sociétés) + Dépréciations & Amortissements – Variations du BFR – Capex
Pour plus d’informations sur le FCFF, vous pouvez vous référer à notre article dédié au Free Cash Flow to Firm.
Les FCFF constituent donc la totalité des cash flows disponibles pour tous les financeurs d’une entreprise. Par conséquent, si vous utilisez les FCFF dans un calcul de Discounted Cash Flow, c’est à dire en remplaçant les “CF” dans la formule du Discounted Cash Flow par les FCFF que vous prévoyez chaque année, la valorisation que vous obtiendrez en résultat sera une valorisation pour la totalité de l’entreprise, c’est à dire pour acheter son capital social et ses dettes.
Cette valeur est ce que l’on appelle communément l’Enterprise Value.
Pour calculer l’Enterprise Value d’une entreprise, il vous suffit de procéder en suivant simplement les étapes ci-dessous :
- Estimer les Free Cash Flows to Firm (FCFF) sur les 5 prochaines années puis un FCFF “à l’infini” que vous pensez réalisable par l’entreprise sur le long terme.
- Estimer un taux de croissance à l’infini de l’entreprise.
- Calculer la valeur terminale comme nous l’avons fait précédemment à partir de ce FCFF à l’infini, du taux de croissance et de votre taux d’actualisation.
- Utilisez les 5 FCFF que vous avez estimés pour les 5 prochaines années et la valeur terminale que vous venez de calculer dans la formule de Discounted Cash Flow (ou sur Excel avec les formules VAN ou VAN.PAIEMENT) pour calculer l’Enterprise Value.
L’utilisation des Free Cash Flow to Equity (FCFE) dans le Discounted Cash Flow
Les Free Cash Flow to Equity (abrégés en FCFE) font aussi partie des cash flows très utilisés dans un modèle de Discounted Cash Flow, mais cette fois pour calculer la valeur du capital social (ou equity en angais) de l’entreprise uniquement, et non pas sa valeur totale.
En effet, les FCFE représentent le cash flow disponible pour les actionnaires uniquement, après avoir payé les créanciers c’est à dire les dettes de l’entreprise.
Le FCFE se calcule de la manière suivante :
FCFE = FCFF – Interest Expenses + Capital Increase – Capital Decrease + New Borrowings – Debt Repayment
Ou en français :
FCFE = FCFF – Intérêts + Augmentation de capital – Diminution de capital + Emission de dette – Remboursement de dette
Comme le FCFE représente les cash flows disponibles uniquement pour payer les actionnaires, l’utiliser dans un calcul de Discounted Cash Flow permet de valoriser l’entreprise à l’échelle uniquement de la propriété des actionnaires, c’est-à-dire le capital social, ou equity en anglais.
Cette valeur est ce que l’on appelle communément l’Equity Value.
Pour calculer l’Equity Value d’une entreprise, il vous suffit donc de procéder en suivant simplement les étapes ci-dessous :
- Estimer les Free Cash Flows to Equity (FCFE) sur les 5 prochaines années puis un FCFE “à l’infini” que vous pensez réalisable par l’entreprise sur le long terme.
- Estimer un taux de croissance à l’infini de l’entreprise.
- Calculer la valeur terminale comme nous l’avons fait précédemment à partir de ce FCFE à l’infini, du taux de croissance et de votre taux d’actualisation.
- Utilisez les 5 FCFE que vous avez estimés pour les 5 prochaines années et la valeur terminale que vous venez de calculer dans la formule de Discounted Cash Flow (ou sur Excel avec les formules VAN ou VAN.PAIEMENT) pour calculer l’Equity Value.
Félicitations, vous savez maintenant valoriser une entreprise à l’aide d’un Discounted Cash Flow basé soit sur les FCFF si vous souhaitez l’Enterprise Value, soit sur les FCFE si vous souhaitez l’Equity Value.
La valorisation d’une action en bourse à l’aide d’un Discounted Cash Flow
Imaginons maintenant que vous souhaitiez valoriser une action seulement.
Dans ce cas, il vous faut prendre en compte le cash flow généré par cette action, c’est-à-dire tout simplement son dividende. La démarche est donc exactement similaire à notre exemple précédent sur l’entreprise fictive BigWin Inc.
Vous devez donc estimer les dividendes futurs de l’entreprise qui vous intéresse à partir de ses dividendes passés, des prévisions de ses résultats financiers futurs et utiliser ces estimations de dividendes dans le calcul du Discounted Cash Flow (comme dans notre exemple précédent).
Le cas des Fixed Income (bonds, loyers, etc…)
Comme vous l’avez vu, un calcul de Discounted Cash Flow permet de valoriser n’importe quel actif qui génère des cash flows dans le temps. C’est le cas d’une entreprise dans sa totalité ou d’une action comme nous l’avons vu, mais aussi d’une multitude d’autres actifs financiers.
Par exemple une obligation, c’est à dire une créance (ou une dette) va générer des revenus fixes pour son détenteur, ce que l’on appelle un coupon, jusqu’au moment du remboursement du principal de l’obligation par l’entreprise qui l’a émise.
C’est donc ces cashs flows (d’abord les coupons puis le remboursement du principal la dernière année) que vous pouvez intégrer dans votre calcul de Discounted Cash Flow pour valoriser cette obligation.
Vous pouvez aussi appliquer un calcul de Discounted Cash Flow à un bien immobilier. Il vous suffit pour cela de calculer les loyers qu’il vous rapportera tous les ans dans votre calcul de DCF.
C’est simple : les DCF permettent de valoriser toutes les classes d’actifs. C’est là toute la puissance de cette méthode et la raison qui fait sa popularité dans le monde la finance et de l’investissement.
Choisir le bon taux d’actualisation
Dans la formule du Discounted Cash Flow nous avons vu quels sont les cash flows à choisir en fonction de ce que vous souhaitez valoriser, mais il reste encore à définir votre taux d’actualisation.
La première règle à respecter est de toujours choisir un taux d’actualisation (ou discount rate en anglais) en ligne avec les cash flows que vous avez choisis, pour ne pas mélanger les choux et les carottes comme le dit un proverbe un peu ringard mais terriblement juste.
L’utilisation du WACC dans le Discounted Cash Flow
Le WACC pour Weighted Average Cost of Capital (ou CMPC en français pour Coût Moyen Pondéré du Capital), est le coût de financement d’un investisseur, entreprise ou autre.
On le calcule comme une moyenne entre les deux types de financement qui existent : Equity et Debt.
La formule du WACC est donc la suivante :
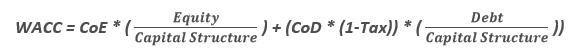
où :
- CoE = Cost of Equity ;
- CoD = Cost of Debt ;
- 1-Tax = Tax Shield ;
- Capital Structure = Equity + Debt.
Pour plus de précisions sur le calcul du WACC, vous pouvez vous référer à notre article dédié à ce sujet en cliquant ici.
Le WACC s’utilise donc toujours avec les Free Cash Flow to Firm (FCFF) dans un calcul de Discounted Cash Flow pour calculer l’entreprise value d’une société.
Si vous prenez un peu de recul, c’est tout à fait logique : comme nous l’avons vu, les FCFF sont les cash flows disponibles pour les actionnaires et les créanciers. Il est donc logique de les diviser par un taux d’actualisation qui est une moyenne entre le coût de l’equity, en ce qui concerne les actionnaires, et de la dette, en ce qui concerne les créanciers.
L’utilisation du Cost of Equity dans le Discounted Cash Flow
L’autre taux d’actualisation que nous utilisons souvent dans un calcul de Discounted Cash Flow est le coût du capital, ou cost of equity en anglais.
Contrairement au WACC, il ne prend en compte que le coût de financement en Equity.
Vous l’avez donc peut-être deviné, nous l’utilisons généralement pour calculer l’Equity Value, donc avec les Free Cash Flow to Equity.
Le but est de toujours rester cohérent entre le numérateur et le dénominateur de chaque membre de la somme dans la formule du Discounted Cash Flow. Si nous utilisons au dénominateur les FCFE, qui représentent les cash flow disponibles uniquement aux actionnaires, il est logique de prendre au dénominateur le Cost of Equity.
Le RRR – Required Rate of Return
Enfin, le dernier taux que nous utilisons généralement dans un calcul de Discounted Cash Flow est le Required Rate of Return (RRR) aussi appelé Taux de Rendement Exigé (TRE) en français.
Le RRR représente le taux de rendement minimal qu’un investisseur souhaite générer avec l’investissement qu’il envisage.
Il dépend de chaque entreprise et de chaque investisseur.
Par exemple, imaginons que l’entreprise BigWin Inc souhaite investir dans un nouveau projet.
Son WACC, c’est à dire son coût de financement, pour investir dans ce projet est de 5%.
Si BigWin Inc veut générer au moins 1,5% de marge bénéficiaire au-dessus de son WACC, elle va exiger un taux de rendement de 6,5% sur ce projet (5% de WACC plus 1,5% de marge bénéficiaire, aussi appelée création de valeur).
Elle va donc calculer un Discounted Cash Flow avec en numérateur tous les cash flows générés par son projet et en dénominateur un taux d’actualisation qui sera son RRR (ou TRE) de 6,5%.
La valorisation calculée sera le montant maximum que le projet doit lui coûter pour générer une rentabilité de 6,5%, soit le taux de rentabilité que les dirigeants de BigWin Inc exigent au minimum de leurs investissements.
Compléter vos valorisations par les DCF avec des multiples de valorisation
Vous savez maintenant valoriser n’importe quel investissement ou actif grâce à la méthode des Discounted Cash Flow.
Ce n’est cependant pas la seule méthode de valorisation qui existe. Vous pouvez notamment utiliser une autre méthode de valorisation très célèbre : la méthode des multiples de valorisation.
Cela tombe bien, nous vous avons rédigé un article complet sur les multiples de valorisation pour vous aider à les comprendre et à les utiliser.
C’est bien simple, avec The Big Win, l’évaluation, l’analyse financière et les valorisations n’auront plus de secret pour vous !



 Suivez-nous sur LinkedIn et Instagram pour plus de contenu et conseils :
Suivez-nous sur LinkedIn et Instagram pour plus de contenu et conseils :


Bonjour,
Premièrement, un grand merci pour tous les articles que vous avez produit dernièrement. Ils sont vraiment bien expliqués, les exemples sont concrets, les sujets variés… bref, c’est topissime ! merci beaucoup !
Petite remarque sur le calcul de la Terminal Value.
Si je reprends votre exemple,
cash flow « Infini » = 4€
taux actualisation = 5%
taux de croissance = 2%
Selon vos explications,
Terminal Value = 4 / (5% – 2%) = 133,33 €
Si j'applique la méthode qui m'est enseigné en MSc Corporate Finance, j'obtiens un résultat différent …. voici la démarche que nous utilisons
dernier cash flow : 5€
taux de croissance : 2%
taux d'actualisation : 5%
On défini le cash flow "infini" en projetant le dernier cash flow avec le taux de croissance, ce qui donne : 5 * (1+2%)
Ainsi la formule complète donne : 5 * (1+2%) / 5% – 2% = 170€
Ma question ne concerne pas forcément l'écart de valorisation car tout dépend des hypothèses faites pour les projections… en revanche, je me demande pourquoi vous avez défini un cash flow "infini" de 4€ sachant que le dernier cash flow estimé est de 5€ et le taux de croissance de 2€ ?
J'éspère que ma question est suffisamment claire …
Merci !
Bonjour Olivier,
En fait les deux calculs sont justes, c’est simplement une différence d’énoncé entre l’exemple de notre article et celui tiré de ton MSc.
Dans l’exemple que tu prends l’énoncé ne semble pas te donner de cash flow à l’infini spécifique, il est donc logique de prendre le dernier en date (5€), de lui incrémenter une année de croissance pour le transformer en un cash flow de terminal value l’année suivante à discounter à l’infini par (5% – 2%).
Dans notre cas nous avons fait une hypothèse de cash flow à l’infini de 4€ en se basant sur une analyse financière que nous imaginons dans notre exemple, raison pour laquelle nous utilisons ce montant de 4€ dans notre calcul de terminal value.
Ces différences montrent en revanche une chose importante : la finance, et en particulier la valorisation, est plus un art qu’une science. La seule règle dans vos calculs est de coller le plus possible à la réalité financière de la situation que vous analysez. Si tous les signes montrent que le dividende à l’infini sera de 4€ il vaut mieux utiliser cette valeur dans la terminal value plutôt que le dividende de l’année précédente qui survaloriserait la société. Si vous n’avez pas de meilleure estimation alors utiliser le dernier cash flow disponible comme dans ton exemple est la meilleure solution.
Pour cela la meilleure chose à faire est de bien comprendre comment sont construites les formules pour pouvoir les utiliser spécifiquement au cas qui vous intéresse.
Justement, concernant la terminal value nous y avons consacré un article complet pour expliquer d’où elle vient (c’est en fait le résultat d’une série géométrique convergente) et comment l’estimer : notre article sur la terminal value.
Merci beaucoup ! explication claire et précise !