Si vous souhaitez travailler en finance, que ce soit en corporate finance ou en finance de marché, vous serez sans doute confrontés à la notion de taux sans risque, aussi souvent appelée par sa traduction anglaise : risk-free rate. 

En effet, le taux sans risque est le point de départ de presque tous les calculs de taux d’intérêts ou de rendements et par conséquent, des taux exigés par les investisseurs. 

Il est donc utilisé sur les marchés de dettes, d’actions mais aussi de private equity ou en M&A. 

Pas d’inquiétudes, The Big Win vient à votre secours pour vous expliquer tout ce que vous devez savoir sur la notion de taux sans risque : définition, formule ou utilisations. C’est parti !  

Taux sans risque : définition et explications 

Le taux sans risque est le taux de rendement pour un investissement considéré comme sûr, c’est-à-dire sans aucun risque de défaut.  

Cela signifie que vous n’avez aucun risque que l’emprunteur fasse faillite et par conséquent, ne puisse pas rembourser son emprunt. 

La notion de taux sans risque est par conséquent intimement lié à ce que l’on appelle en finance le rapport risque-rendement, ou risque-rentabilité, qui symbolise la notion de rémunération du risque.  

Cette notion est basée sur le fait que plus un investissement est considéré comme risqué, plus il doit apporter une rentabilité élevée pour convaincre des investisseurs.  

C’est tout à fait logique, voici un exemple : si vous avez 100€ à investir et que vous avez le choix entre deux investissements dans deux entreprises, A et B, qui vous promettent toutes les deux une rentabilité de 10% mais que l’entreprise A est très solide alors que l’entreprise B affiche un risque beaucoup plus élevé. Pourquoi iriez-vous investir dans l’entreprise B et prendre plus de risques pour une rentabilité similaire ? Cela n’a aucun intérêt. 

Ainsi, pour vous convaincre d’investir chez elle, l’entreprise B devra vous proposer une rentabilité supérieure à l’entreprise A, par exemple 15% au lieu de 10%. Après, ce sera à vous de voir si vous êtes prêts à prendre plus de risques pour plus de rentabilités. 

On peut donc résumer le principe de tout investissement financier comme suit : plus de risques = plus de rentabilités. 

Maintenant que nous avons vu cette notion de rémunération du risque, la notion de taux sans risque devient beaucoup plus naturelle : c’est le rendement que vous pouvez obtenir pour un investissement avec un niveau de risque nul. 

Pour illustrer cette théorie, voici donc un graphique qui met en relation risque et rendement comme nous l’avons vu. Attention : tous ces chiffres sont parfaitement fictifs, ne les utilisez pas dans vos travaux professionnels ou académiques. 

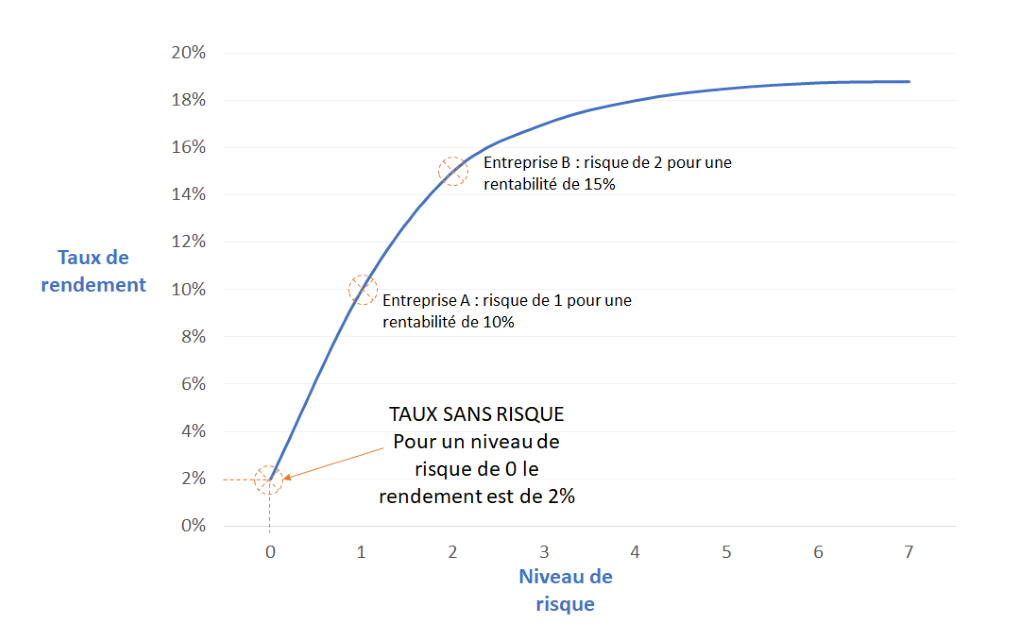
On voit donc que le taux sans risque, c’est-à-dire le rendement d’un investissement parfaitement sûr, est de 2%. Si au contraire, vous investissez dans l’entreprise A, qui comme toute entreprise est un investissement qui contient une part de risque (en premier lieu, le risque que l’entreprise fasse faillite), alors le rendement est de 10%. Enfin, l’entreprise B, qui présente un profil de risque 2 fois plus élevé que l’entreprise A (par exemple, parce que c’est une jeune start-up), alors le rendement augmente à 15%. 

Utilisations du taux sans risque 

Maintenant que nous avons vu ce qu’est le taux sans risque, voyons à quoi il sert. 

Calculer son Cost of Equity 

La première utilité du taux sans risque est de calculer son Cost of Equity. En effet, comme nous l’avons vu, un taux de rendement correspond à un certain niveau de risque. Par conséquent, chaque investissement qui présente un minimum de risque peut être décomposé en une somme de deux taux : le taux sans risque et un complément de rentabilité pour rémunérer le risque supplémentaire. 

Grâce à ce raisonnement, il devient beaucoup plus aisé de définir les composantes d’un cost of equity : 

Cost of Equity = Taux sans risque + Prime de risque 

ou en anglais : 

Cost of Equity = Risk free rate + Risk premium 

Maintenant que vous connaissez la formule ci-dessus, vous pouvez calculer la rentabilité exigée pour n’importe quelle action, obligation ou tout autre produit financier. 

Ainsi, il vous suffit de définir le niveau de risque d’une entreprise, de regarder comment les marchés financiers rémunèrent un niveau de risque équivalent, et d’y ajouter le taux sans risque pour obtenir le cost of equity qui vous intéresse. 

Cette méthode est principalement utilisée par les brokers et banques d’affaires tant sur les marchés actions que sur les marchés obligations puisque le rendement d’une obligation peut être découpée exactement de la même manière. 

Vous vous demandez peut-être comment calculer la prime de risque puisque nous n’avons pas encore précisément abordé ce point. Nous y venons justement. Pour y parvenir, il vous faut deux métriques supplémentaires : 

• Le bêta de votre action : A chaque action, nous pouvons attribuer un bêta, noté β. Ce bêta est le coefficient qui représente le rapport entre les évolutions de marché et les évolutions de prix de votre action. Par exemple, si à chaque fois que le marché augmente de 5% votre action a tendance à augmenter de 10% alors le bêta de l’action est de 2. Ce bêta est une mesure de risque, puisqu’il représente la volatilité de votre action par rapport à la volatilité du marché.  
• Le rendement moyen historique du marché de votre action : Choisissez le bien ! Il faut que ce marché soit comparable au profil de votre entreprise. Par exemple, ne prenez pas le rendement du CAC40 si vous travaillez sur une start-up. Il faut aussi que ce soit le même marché que celui avec lequel vous avez calculé votre bêta. Dans notre exemple précédent, il s’agit donc du marché qui augmente de 5% quand votre action augmente de 10%. 

Une fois que vous avez ces deux données supplémentaires, vous pouvez donc appliquer la formule suivante : 

Cost of Equity = Taux sans risque + β * (Rendement moyen du marché – Taux sans risque) 

Ou en anglais : 

Cost of Equity = Risk free rate + β * (Average market return – Risk free rate) 

Prenons un exemple pour mieux illustrer ce schéma de calculs. Imaginons l’entreprise BigWin Inc, cotée au NASDAQ et qui a les métriques suivantes : 

• L’année dernière, le NASDAQ a augmenté de 10% (le chiffre est fictif). 
• A chaque mouvement de 1% du NASDAQ, le cours de BigWin Inc évolue de 1,5% en moyenne. On en déduit donc que le bêta de BigWin Inc est de 1,5 (Bêta BigWin Inc = évolution cours BigWin Inc de 1,5% divisé par évolution cours NASDAQ de 1%). 
• Le taux sans risque est de 2%. 

Dans ce cas, le rendement exigé pour BigWin Inc est le suivant : 

2% + 1,5 * ( 10% – 2% ) = 14% 

Pour établir des benchmarks 

Le taux sans risque peut aussi servir à établir des benchmarks. En effet, en gestion d’actifs, l’objectif d’un gérant est de faire fructifier son portefeuille pour obtenir le meilleur rendement possible en respectant le cadre de son mandat de gestion. 

Cependant, il faut un peu plus de subtilités pour évaluer la performance financière d’un gérant que de simplement dire “le plus gros rendement possible”. 

Que pensez-vous d’un gérant qui affiche une performance de 3% si le taux sans risque est aussi de 3% ? Ce n’est pas si formidable que ça non ? 

C’est pour cette raison que la plupart des performances financières se calculent sur la marge générée au-dessus du taux sans risque. Sinon pourquoi ne pas tout simplement placer votre investissement sur un produit sans risque et obtenir le même rendement ? 

Établir le rendement de certains produits dérivés et contrats financiers à partir du taux sans risque 

Exactement comme nous avons décortiqué le Cost of Equity en différentes composantes qui incluent le taux sans risques; les banques d’affaires, lorsqu’elles proposent des produits financiers à leurs clients Corporates, établissent souvent le prix de ces produits en se basant notamment sur le taux sans risque. 

Ici, nous ne parlons pas de prix en euros, dollars ou livres sterling, mais en taux.  

Les premiers composants de ces produits financiers sont tout simplement… les emprunts. Contrairement à un emprunt pour un particulier, lorsqu’une banque d’affaires propose un taux d’emprunt à un client corporate, elle ne lui indique jamais un taux d’intérêt fixe, de but en blanc.  

En général, elle indique à son client un taux qu’elle va lui facturer en plus du taux sans risque.  

Prenons encore un exemple. Mettons que l’entreprise BigWin Inc soit une entreprise d’énergies renouvelables qui construit et exploite des parcs solaires. Pour développer son prochain parc, elle prospecte différentes banques pour emprunter les montants nécessaires à l’achat de matériel et à la construction. 

Il y a toutes les chances pour que les banques qui lui répondent ne lui proposent pas un taux d’emprunt de 3,5% par exemple mais plutôt un taux qui corresponde au taux sans risque, par exemple 2%, plus une marge, par exemple 1,5%. Vous vous demandez sans doute pourquoi complexifier les choses et ne pas afficher simplement 3,5% : vous avez raison. 

En fait, en décomposant de cette manière le taux d’intérêt dans ses contrats, la banque se protège contre une augmentation du taux sans risque. 

En effet, si au moment de la signature du contrat, le taux sans risque est de 2%, dans ce cas la banque génère son bénéfice grâce au 1,5% de marge en plus de ce qu’elle facture à son client. Le problème est alors le suivant : si dans 20 ans, le taux sans risque est passé de 2% à 3% et que la banque avait proposé 3,5% fixe à BigWin Inc, alors son bénéfice réel ne sera plus que de 0,5%. 

A contrario, en lui présentant un contrat avec comme taux d’intérêt, le taux sans risque plus 1,5%, si, dans 20 ans, le taux sans risque est de 3%, BigWin Inc devra payer 4,5% d’intérêts (3% + 1,5%). Ainsi, la banque sera certaine de conserver sa marge de 1,5%. En procédant de la sorte, les banques sont assurées de préserver leurs marges, quelle que soit l’évolution du taux sans risque. 

Comment bien choisir et calculer son taux sans risque 

Maintenant que vous savez ce qu’est le taux sans risque et son utilité, il reste encore à choisir ce taux. 

En effet, dans nos différents exemples, nous avons pris arbitrairement 2% sans vous donner plus de précisions sur sa provenance. 

En fait, il y a plusieurs manières de choisir son taux sans risque et nous allons vous expliquer les trois principales. 

Utiliser les obligations d’Etat 

Maintenant que vous connaissez la définition du taux sans risque, à savoir le taux de rentabilité d’un investissement considéré comme sûr, encore faut-il trouver un tel investissement. 

La première possibilité est tout simplement de prendre le taux d’intérêt payé par les obligations d’Etats considérés comme non risquées. En général, il s’agit donc des Etats les plus développés et stables financièrement parlant : Etats-Unis, Allemagne, Japon, France, Royaume-Uni, etc… 

On considère en effet que ces Etats ne risquent pas de faire défaut et paieront donc toujours leurs dettes. Si vous analysez une entreprise française, vous pouvez donc prendre comme taux sans risque le taux d’intérêt des obligations de l’Etat français. Le nom officiel de ces obligations est “Obligation Assimilable au Trésor”, généralement abrégé en OAT.  

Attention cependant, il existe des obligations d’Etats de maturités différentes, qui correspondent donc à la durée de l’emprunt correspondant à cette obligation : 3 mois, 6 mois, 1 an, 2 ans, 5 ans, 10 ans, etc…  Pour les OAT françaises, leur maturité va de 2 à 50 ans.

Il convient donc de choisir le taux d’une obligation avec une maturité en cohérence avec la durée de votre propre investissement. 

En ce qui concerne la France, vous pouvez retrouver les taux des OAT sur le site de la Banque de France en cliquant ici. 

Le LIBOR comme taux sans risque à l’international

Il existe une deuxième manière de définir son taux sans risque, qui est plus souvent utilisée par les banques, notamment lorsqu’elles définissent le taux auquel elles prêtent à leurs clients. Cette deuxième solution est de prendre le taux du LIBOR.  

En résumé, le LIBOR est le taux auquel les banques se prêtent de l’argent entre elles. LIBOR est l’acronyme de London Interbank Offered Rate. Il est calculé tous les jours et publié par l’agence Thomson Reuters en cinq devises : Dollars (USD), Livre Sterling (GBP), Yen (JPY), Franc Suisse (CHF) et Euro (EUR).  

Comme pour les obligations d’Etats il existe plusieurs maturités pour le LIBOR : 1 jour, 1 semaine, 2 semaines, 1 mois, 2 mois, 3 mois, etc… jusqu’à 12 mois. 

Choisissez donc le taux dont la maturité correspond le mieux à la durée de votre investissement. 

Concrètement, si nous reprenons notre exemple précédent dans la partie “Etablir le rendement de certains produits dérivés et contrats financiers à partir du taux sans risque”, lorsque la banque va répondre à BigWin Inc pour proposer un prêt, sa proposition sera sous la forme suivante “Nous vous proposons un prêt de 10 M€ au taux LIBOR 3 mois + 1,5%”. 

L’EURIBOR comme référence de taux sans risque en zone Euro

Il est enfin possible de définir le taux sans risque sur la base de l’EURIBOR. La méthode est strictement la même que pour le LIBOR, c’est-à-dire que nous prenons comme taux sans risque, le taux de l’EURIBOR sur la maturité qui nous intéresse. 

L’EURIBOR, acronyme de Euro Interbank Offered Rate ou Taux Interbancaire Offert en Euro (TIBEUR) en français, est le taux auquel les banques se prêtent de l’argent entre elles sur le marché Euro.  

Il fait donc office de taux de référence comme taux sans risque dans la zone Euro et est ainsi plus souvent utilisé que le LIBOR dans les pays qui utilisent la monnaie de l’Union Européenne. 

Limitations du taux sans risque 

La principale limitation du taux sans risque concerne le fait de choisir les obligations d’Etat pour le définir. En effet, il est de plus en plus fréquent de voir les Etats les plus solides financièrement parlant emprunter à des taux négatifs. Dans ce cas, il est difficile d’utiliser le taux d’une obligation d’Etat, comme une OAT en France, pour définir son taux sans risque. 

La deuxième difficulté est justement de choisir la bonne référence. La référence que vous choisirez peut dépendre de votre localisation géographique, de la monnaie que vous utilisez et de la durée choisie. 

Ainsi, vous n’allez pas utiliser le taux d’emprunt de l’Etat Japonais pour définir un taux sans risque en France ; cela n’aurait aucun sens. 

Par conséquent, choisissez une référence en cohérence avec l’investissement ou l’opération financière que vous envisagez. Si c’est en Europe et en Euro, pensez à l’EURIBOR. Sinon, le LIBOR est une excellente solution car il est utilisé dans la plupart des pays du monde et reste une référence très fiable.