Le TRI (Taux de Rentabilité Interne) est un indicateur essentiel et mondialement connu (en anglais, « IRR » ou « Internal Rate of Return ») quand il s’agit de calculer la rentabilité d’un projet. Le calcul du TRI est donc vraiment une notion incontournable pour celles et ceux qui souhaitent faire carrière en finance d’entreprise ou dans l’entrepreneuriat.
Néanmoins, son utilisation est très souvent critiquée dans le monde de la finance et le TRI ne peut être retenu comme seul indicateur financier lors d’une décision d’investissement. Par ailleurs, TRI et VAN (Valeur Actuelle Nette) sont indissociables ! Le TRI et la VAN sont des concepts encore flous dans votre esprit ? Pas de problèmes ! On vous explique tout sur le calcul TRI dans cet article !
- Le résumé de l’article en vidéo
- Le calcul du TRI, qu’est-ce que c’est ?
- Calcul du TRI : la formule à connaitre par cœur
- Calcul du TRI : les applications
- Les limites du calcul du TRI
- La VAN, qu’est-ce que c’est ?
- Calcul du TRI et rapport avec la VAN
- Calcul du TRI : deux interprétations possibles pour l’appeler « le taux qui annule la VAN »
- Calcul du TRI à comparer au TRE
- Calcul du TRI : faut-il toujours opter pour le TRI le plus élevé ?
- La notion de temps dans le calcul TRI
- Quel indicateur faut-il donc retenir entre le calcul du TRI et la VAN ?
- Le TRI dans un contexte macro-économique international changeant
Le résumé de l’article en vidéo
Le calcul du TRI, qu’est-ce que c’est ?
Les projets d’investissement sont des composantes très importantes de la croissance d’une entreprise. Nous prendrons l’exemple d’une entreprise qui décide de développer une nouvelle activité et qui, pour ce faire, a besoin de construire une nouvelle usine. Pour permettre la construction de cette usine, l’entreprise va devoir engager des CAPEX (« Capital Expenditure »), autrement dit, des dépenses de construction. Les flux de trésorerie qui seront générés par cette nouvelle usine et perçus par l’entreprise, permettront de rembourser ce CAPEX initial. Notez que les CAPEX peuvent être aussi bien financés par de la dette que par des fonds propres.
Avant de lancer une construction, une analyse d’investissement doit être menée afin de déterminer la rentabilité du projet en question. C’est, précisément à ce moment-là, que le calcul TRI prend toute son importance. Le TRI est un indicateur financier qui mesure la rentabilité d’un investissement. Le calcul TRI va prendre en compte le CAPEX initial (flux négatif) et les flux de trésorerie dégagés par la nouvelle usine (flux positifs). Le calcul TRI permet ainsi de calculer la rentabilité de l’investissement en comparant les dépenses initiales de CAPEX et les excédents de trésorerie perçus.
Notez que le TRI est le taux qui annule la VAN (c’est-à-dire que la VAN est égale à zéro). En théorie, pour que le projet apporte une valeur ajoutée à l’entreprise qui le construit, il faut que le TRI soit supérieur au WACC de l’entreprise. On étudie en détails ce sujet dans le chapitre de la VAN, un peu plus bas, dans cet article.
Calcul du TRI : la formule à connaitre par cœur
Non ! Nous n’allons pas vous sortir une formule compliquée avec des signes incompréhensibles.
En fait le calcul du TRI est tout simplement trop complexe à réaliser « à la main ». En effet, cela voudrait dire résoudre une équation (la formule de la VAN avec le taux comme inconnu et la VAN égale à 0) avec de nombreuses puissances.
C’est évidemment faisable mais inutilement long et complexe.
Par conséquent le calcul du TRI se fait concrètement avec des calculatrices financières et le plus souvent à l’aide… d’Excel tout simplement !
Ainsi nous allons droit au but : le calcul TRI s’effectuera avec les formules Excel « TRI » et « TRI.PAIEMENTS ». Nous préfèrerons la formule TRI.PAIEMENTS qui prendra en compte la « timeline » du projet (c’est-à-dire les dates auxquelles se réfèrent les flux financiers) et qui, par conséquent, sera plus précise. Mais ne soyez pas surpris de croiser la formule TRI dans les modèles financiers que vous analyserez. La formule TRI est correcte mais juste moins précise car elle ne tient pas compte des dates.
Formule « TRI » sur Excel
La Formule du TRI est la suivante :
= TRI (valeurs)
Où :
Les « valeurs » sont les flux générés par le projet (FCFF ou FCFE).
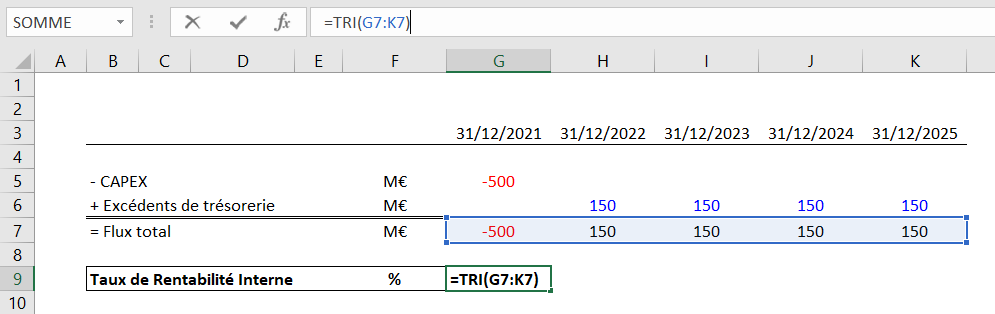
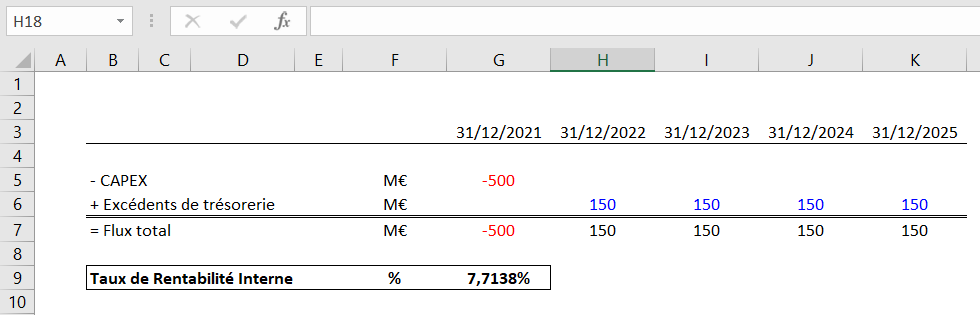
Nous obtenons un TRI de 7,7138% avec cette première formule « TRI », la plus simple d’Excel, pour calculer le taux de rendement interne.
Formule « TRI.PAIEMENTS » sur Excel
La Formule du TRI.PAIEMENTS est la suivante :
= TRI.PAIEMENTS (valeurs ; dates)
Où :
- Les « valeurs » sont les flux générés par le projet (FCFF ou FCFE) ;
- Les « dates » sont les dates auxquelles sont générés les flux.
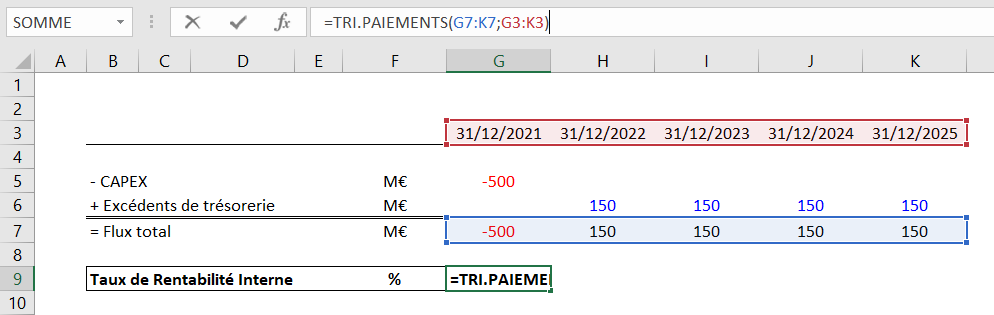
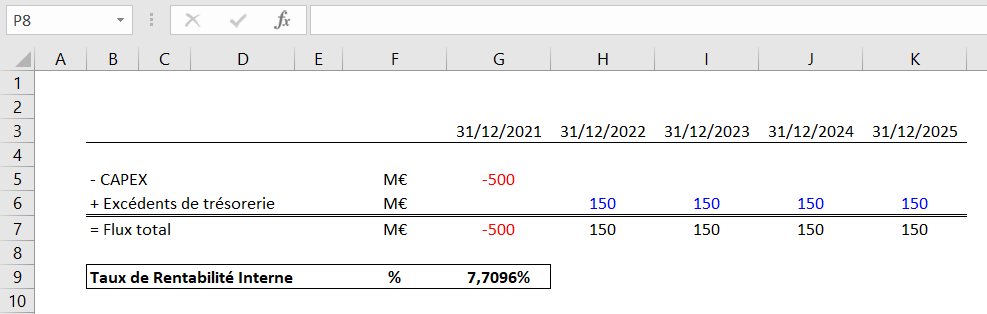
Nous obtenons un TRI de 7,7096%, légèrement différent du TRI obtenu par la formule « TRI ». Comme énoncé, la différence provient de l’utilisation de la formule TRI.PAIEMENT qui prend en compte les dates d’occurrence des cash-flows et permet d’obtenir un TRI plus précis.
Notez que dans le milieu professionnel, nous recommandons d’utiliser la formule TRI.PAIEMENT plutôt que la formule TRI.
NB : pour les formules de TRI, Excel vous proposera d’insérer une « estimation ». Vous pouvez renseigner un taux que vous estimerez être le plus proche du TRI. Cet argument est facultatif et n’empêchera pas la formule de fonctionner correctement si vous l’omettez. L’estimation était autrefois utilisée car elle permettait de calculer un TRI plus rapidement. En effet, la puissance des ordinateurs de l’époque ne permettait pas de calculer des TRI en une fraction de seconde comme aujourd’hui.
Calcul du TRI : les applications
Le TRI s’appliquera aussi bien sur des Free Cash-Flows to Firm que sur des Free Cash-Flows to Equity.
Nous parlerons donc de « TRI projet » lorsqu’il sera calculé sur la base du Free Cash-Flow to Firm et de « TRI Equity » lorsqu’il sera calculé à partir du Free Cash-Flow to Equity.
Free Cash-Flow to Firm (« FCFF ») : c’est le flux qui va rémunérer tous les investisseurs de l’entreprise, c’est-à-dire tous les apporteurs en fonds propres (Equity) et tous les apporteurs en dettes (Debt).
FCFF = EBIT * (1-Tax) + Depreciation & Amortization – Changes in Working Capital – Capital Expenditures
Free Cash-Flow to Equity (« FCFE ») : c’est le flux qui va rémunérer uniquement les investisseurs en fonds propres.
FCFE = FCFF – Interest Expenses + Capital Increase – Capital Decrease + New borrowings – Debt repayment
Les limites du calcul du TRI
Comme évoqué en introduction, le TRI est très critiqué dans le monde de la finance. En effet, selon beaucoup d’analystes, la décision d’investissement d’un projet ne peut se limiter à la seule analyse du TRI. Le TRI n’est, ni plus ni moins qu’un taux pour laquelle la Valeur Actuelle Nette est égale à zéro.
Il ne permet pas de déterminer si, par le biais de la construction du projet, l’entreprise va créer ou détruire de la valeur. C’est principalement pour cette raison que l’analyse du TRI doit être complétée par une analyse de la VAN.
La VAN, qu’est-ce que c’est ?
La VAN (en anglais, « NPV » ou « Net Present Value ») est la somme des flux actualisés d’un projet. Pour rappel, actualiser un cash-flow consiste à calculer la valeur actuelle d’un cash-flow qui sera perçu dans le futur, par exemple pour calculer une valorisation.
Autrement dit, la VAN est la totalité de l’argent qui sera générée par un projet auquel on retire l’investissement initial.
L’analyse de la VAN
Lors de l’analyse d’un projet, l’étude de la VAN conduira les analystes aux conclusions suivantes :
- Une VAN négative : les flux actualisés du projet ne permettent pas de repayer l’investissement initial. Un projet qui présente une VAN négative est un projet qui n’est donc pas rentable. Mathématiquement, la somme des flux actualisés est inférieure au montant de l’investissement initial. Autrement dit, il ne faut surtout pas investir car le projet va détruire de la valeur !
Exemple : un investissement de 500M€ pour une somme de flux actualisés égale à 450M€ (VAN = -50M€).
- Une VAN égale à zéro : lorsque le projet génère une VAN égale à zéro, cela signifie que le projet permet de récupérer l’investissement initial mais n’est pas assez rentable pour créer de la valeur. Mathématiquement, la somme des flux actualisés est égale au montant de l’investissement initial. Une VAN égale à zéro représente le point d’équilibre du projet où aucune perte ne sera constatée et aucun bénéfice ne sera réalisé.
Exemple : un investissement de 500M€ pour une somme de flux actualisés égale à 500M€ (VAN = 0M€).
- Une VAN positive : les flux actualisés du projet permettent de repayer l’investissement initial. Un projet avec une VAN positive est un projet dans lequel il faut investir car il est rentable. Mathématiquement, la somme des flux actualisés est supérieure au montant de l’investissement initial. En effet, un projet avec une VAN positive est un projet qui va créer de la valeur pour l’entreprise !
Exemple : un investissement de 500M€ pour une somme de flux actualisés égale à 550M€ (VAN = 50M€).
La Formule de la VAN
Encore une fois, pas de formules algébriques ici ! On vous explique comment calculer une VAN de manière professionnelle. Le calcul de la VAN s’effectuera avec les formules Excel « VAN » et « VAN.PAIEMENTS ». Comme pour le TRI, nous préfèrerons la formule VAN.PAIEMENTS qui prendra en compte la « timeline » du projet (c’est-à-dire les dates auxquelles se réfèrent les flux financiers) et qui, par conséquent, sera plus précise.
Avant toute chose, sachez qu’une VAN se calcule avec un taux d’actualisation. Ainsi, vous actualiserez vos Free Cash-Flows to Firm avec le Weighted Average Cost Capital (« WACC ») et par opposition, vos Free Cash-Flows to Equity avec le Cost of Equity (« CoE »).
- Pour rappel :
Le Weighted Average Cost of Capital (ou en Français : Coût Moyen Pondéré du Capital (« CMPC ») est le taux de rentabilité annuel moyen attendu par tous les investisseurs de l’entreprise (Equity + Debt).
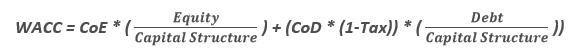
Où :
CoE = Cost of Equity ;
CoD = Cost of Debt ;
1-Tax = Tax Shield ;
Capital Structure = Equity + Debt
Le Cost of Equity (ou en Français : coût des fonds propres) est le taux de rentabilité annuel attendu par les apporteurs de fonds propres (uniquement Equity).
Cost of Equity = Risk-Free Rate + Equity Beta * Risk premium
Où :
Risk premium = Total market return – Risk-Free Rate.
Pour les exemples ci-dessous, nous supposerons un WACC aléatoire de 3,00%.
Formule « VAN » dans Excel
La Formule de la VAN est la suivante :
= VAN (taux ; valeurs)
Où :
Le « taux » est le taux d’actualisation à appliquer (WACC ou CoE) ;
Les « valeurs » sont les flux générés par le projet (FCFF ou FCFE).
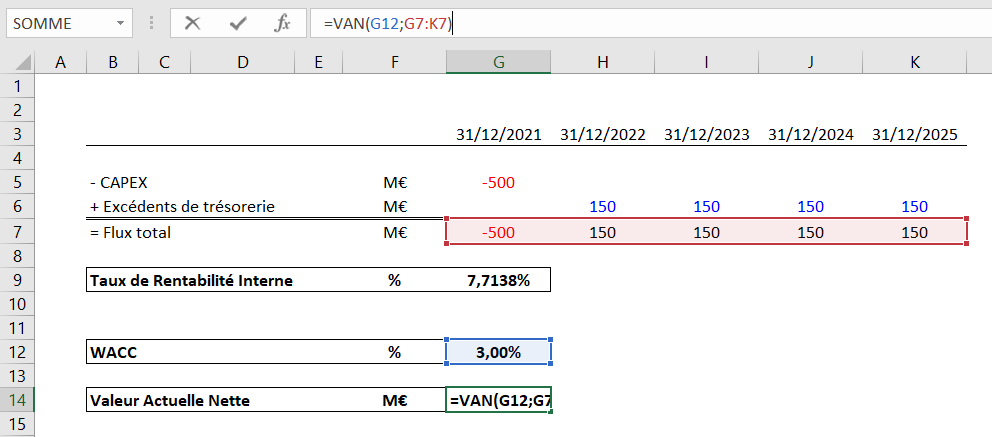
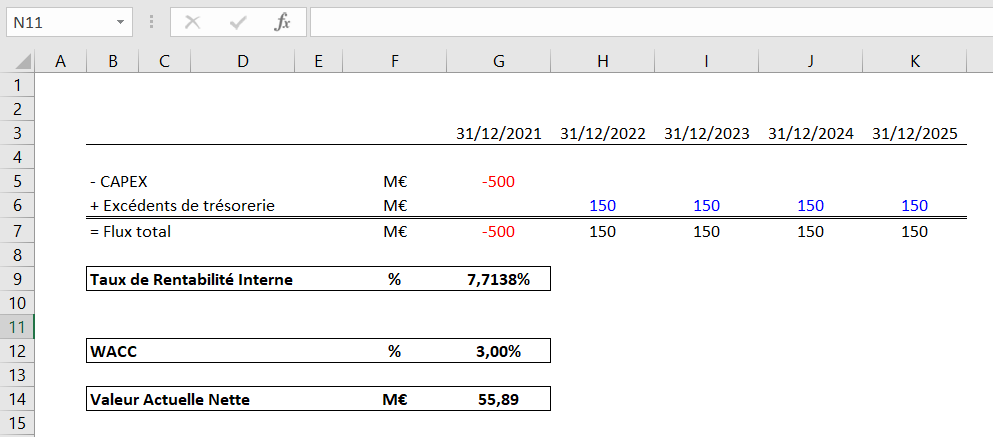
Nous obtenons une VAN de 55,89M€.
Formule « VAN.PAIEMENTS » dans Excel
La Formule de la VAN.PAIEMENTS est la suivante :
= VAN.PAIEMENTS (taux ; valeurs ; dates)
Où :
Le « taux » est le taux d’actualisation à appliquer (WACC ou CoE) ;
Les « valeurs » sont les flux générés par le projet (FCFF ou FCFE) ;
Les « dates » sont les dates auxquelles sont générés les flux.
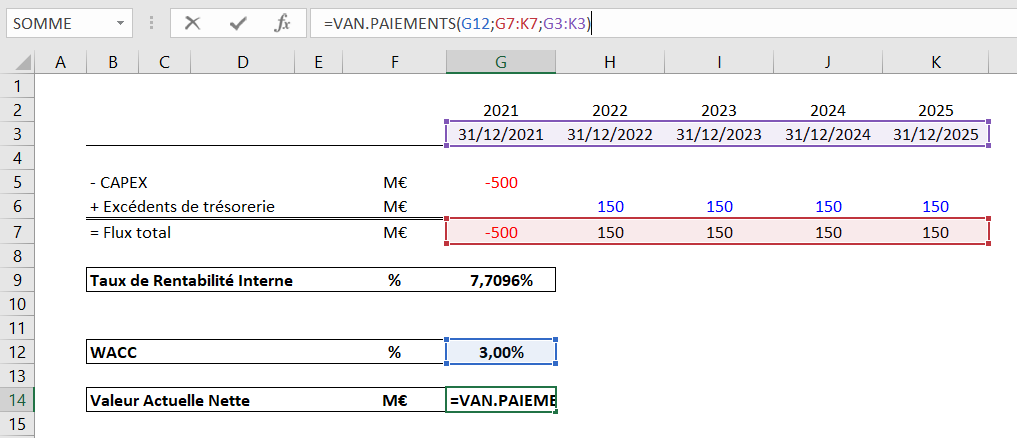
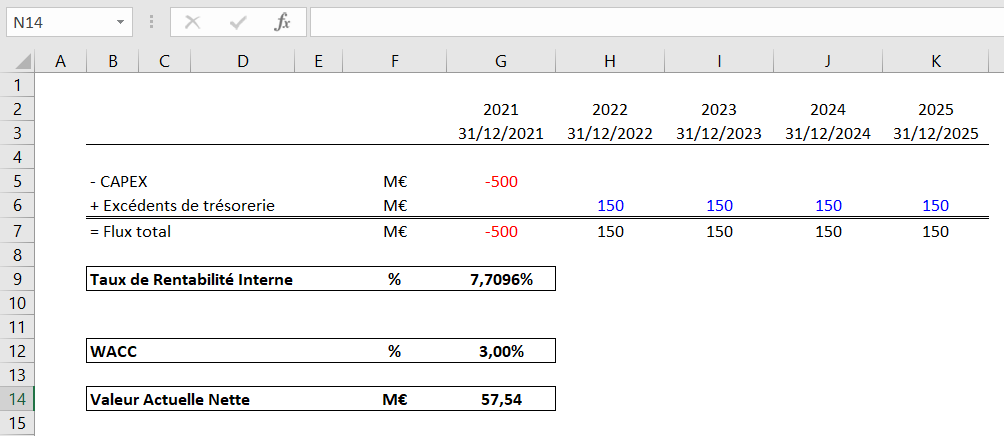
Nous obtenons une VAN de 57,54M€, légèrement différente de la VAN obtenue par la formule « VAN ». Comme énoncé, la différence provient de l’utilisation de la formule VAN.PAIEMENT qui prend en compte les dates d’occurrence des cash-flows et permet d’obtenir une VAN plus précise.
Notez que dans le milieu professionnel, nous recommandons d’utiliser la formule VAN PAIEMENT plutôt que la formule VAN.
Calcul du TRI et rapport avec la VAN
Dans ce chapitre, nous allons vous démontrer que le TRI annule bien la VAN. Nous reprenons notre exemple ci-dessus où :
- TRI = 7,7096%
- WACC = 3,00%
- VAN = 57,54M€
Pourquoi la VAN est positive ?
Il est important de bien comprendre la relation entre TRI, WACC et VAN. Dans notre exemple, la VAN est positive car le TRI du projet est supérieur au WACC de notre entreprise. Pour savoir si le projet lui sera bénéfique, l’entreprise va actualiser les flux du projet avec son propre WACC.
Si nous reprenons la création d’usine dont nous avons pris l’exemple un peu plus haut dans l’article, l’idée est de déterminer si la création de cette nouvelle usine va permettre à l’entreprise de satisfaire la rentabilité de ses actionnaires (rappelez-vous, le WACC est la rentabilité de tous les actionnaires dans une entreprise).
Dans cet exemple, la réponse est oui car les actionnaires attendent une rentabilité de 3,00% tandis que le projet en lui-même permet d’atteindre une rentabilité de 7,71%.
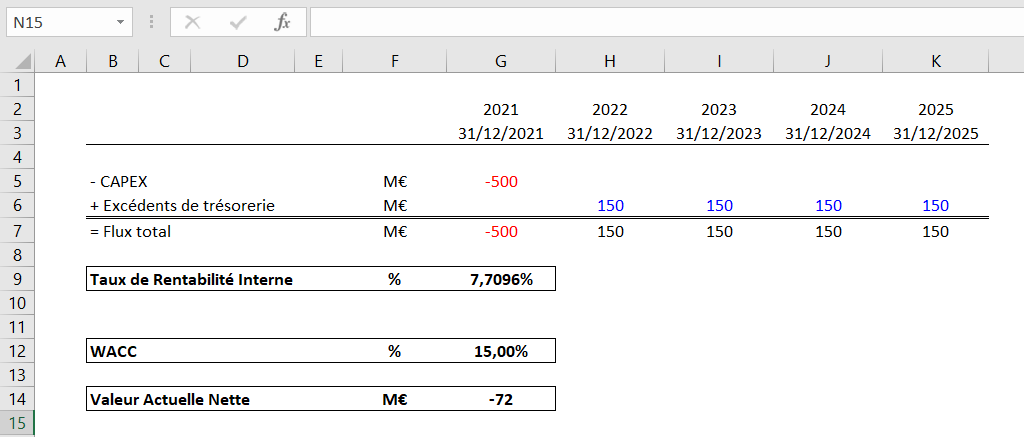
Comment la VAN aurait pu être négative ?
En revanche, si le WACC de l’entreprise avait été de 15,00%, le projet n’aurait pas permis de satisfaire la rentabilité des actionnaires et par conséquent, la VAN aurait été négative. Le TRI est inférieur au WACC et ne permet donc pas à l’entreprise de créer de la valeur car les actionnaires sont trop exigeants.
Comment la VAN est égale à zéro ?
La VAN du projet va être égale à zéro quand la rentabilité des actionnaires va être égale à la rentabilité du projet, autrement dit quand TRI = WACC. Dans ce cas bien précis, l’entreprise a le choix ou non de lancer le projet. Parfois, pour des aspects stratégiques, l’entreprise peut décider d’investir dans un projet où TRI = WACC et par conséquent VAN = 0€. C’est le cas par exemple d’une entreprise qui souhaite pénétrer un nouveau pays ou un nouveau marché.
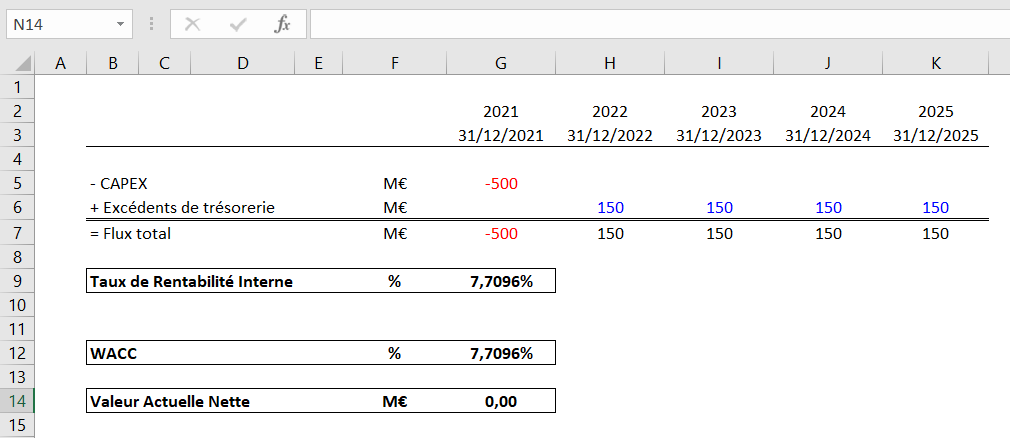
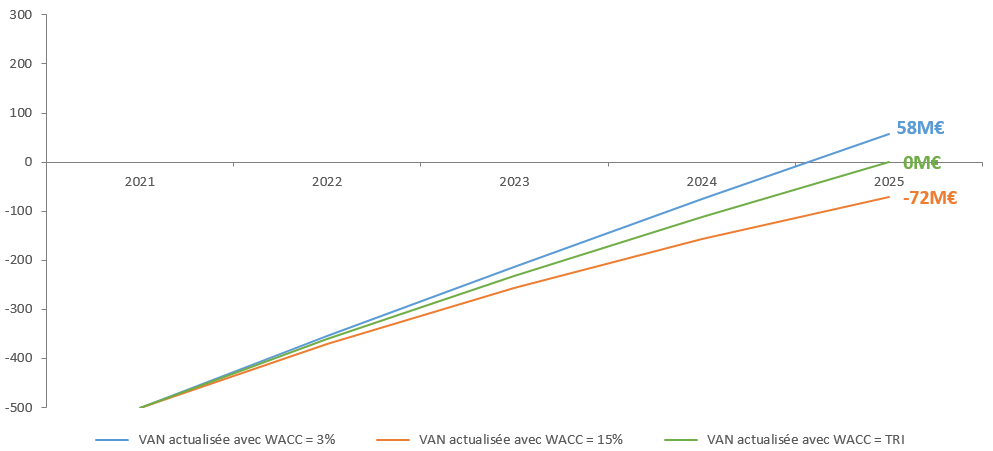
Illustration de tous les cas
Ci-dessous, vous trouverez un graphique regroupant les trois courbes de VAN correspondant aux trois cas étudiés précédemment.
Calcul du TRI : deux interprétations possibles pour l’appeler « le taux qui annule la VAN »
Attention, il y a, selon nous, deux interprétations possibles de la célèbre phrase : « le TRI est le taux qui annule la VAN ».
- La vision purement projet
Si vous raisonnez projet et que vous restez à l’échelle du projet, le TRI est en effet le taux qui annule la VAN. C’est le taux pour lequel le projet ne génère pas de bénéfices mais n’engendre pas de pertes. Lorsque les gens emploient la phrase « c’est le taux qui annule la VAN » pour définir le TRI, c’est, selon nous, à cette vision qu’ils font référence.
- La vision construction du projet par une entreprise
Si vous raisonnez au niveau de l’entreprise qui construit un projet, le TRI est le taux qui annule la VAN quand le TRI est égal au retour attendu des investisseurs (WACC). Le projet ne permet pas aux investisseurs de générer des bénéfices mais ne leur fait pas perdre d’argent pour autant. Dans cette situation bien précise, le TRI du projet permet d’annuler la VAN attendue par l’entreprise.
Calcul du TRI à comparer au TRE
Lors d’une décision d’investissement, le TRI est TOUJOURS comparé au TRE (Taux de Rentabilité Exigée ou Required Rate of Return en anglais).
Comme son nom l’indique, le TRE est un taux de rentabilité exigée par l’entreprise qui souhaite investir. Ainsi, l’entreprise n’investira pas dans un projet dont le TRI sera inférieur à son TRE. Le TRE est calculé à partir du WACC auquel s’ajoute une marge. Par conséquent, le TRE est toujours supérieur au WACC de l’entreprise. Cette marge est appelée la « création de valeur ». En fonction du TRI sélectionné (Projet ou Equity), nous distinguons deux types de TRE :
- Le TRI Projet se compare au TRE Projet
TRE Projet = Weighted Average Cost of Capital + Création de valeur
- Le TRI Equity se compare au TRE Equity
TRE Equity = Cost of Equity + Création de valeur
- La création de valeur
La création de valeur est à la discrétion de chaque entreprise. Ainsi, chaque entreprise appliquera une création de valeur différente. La création de valeur s’exprimera en pourcentage ou en BPS (prononcé « Bips » et qui signifie « Basis point »).
NB : 100 bps = 1%.
Comme le WACC est le coût du capital de l’entreprise (le prix que lui coûte son argent), lorsqu’elle réalise un investissement, elle veut que cet investissement lui rapporte une rentabilité supérieure à son WACC (sinon le projet ne lui rapporte rien). Elle va donc se dire par exemple « notre WACC est de 5%, nous voulons investir dans un projet qui va nous rapporter 2% de plus que notre WACC, par conséquent nous devons appliquer un TRE de 7% ». Les 2% souhaités en plus du WACC représentent sa création de valeur.
Calcul du TRI : faut-il toujours opter pour le TRI le plus élevé ?
La question est totalement légitime. J’ai le choix d’investir sur le Projet 1 qui a un TRI d’environ 5% et sur le Projet 2 qui a un TRI d’environ 8%. A vue d’œil, on aurait tendance à penser qu’il faut absolument investir dans le Projet 1 car son TRI est supérieur de 300bps au TRI du Projet 2. Dans ce chapitre, nous allons vous démontrer que la réponse ne doit pas être aussi précipitée.
Dans les exemples que nous allons vous proposer, nous supposerons à nouveau que le WACC de notre entreprise est égal à 3,00%.
Calcul du TRI et de la VAN du Projet 1
Le projet 1 requiert un investissement de 500M€ et génèrera, sur toute sa durée de vie, 600M€ d’excédents de trésorerie. Le TRI ressort à 4.98% et la VAN est égale à 37M€ actualisée avec un WACC de 3%.
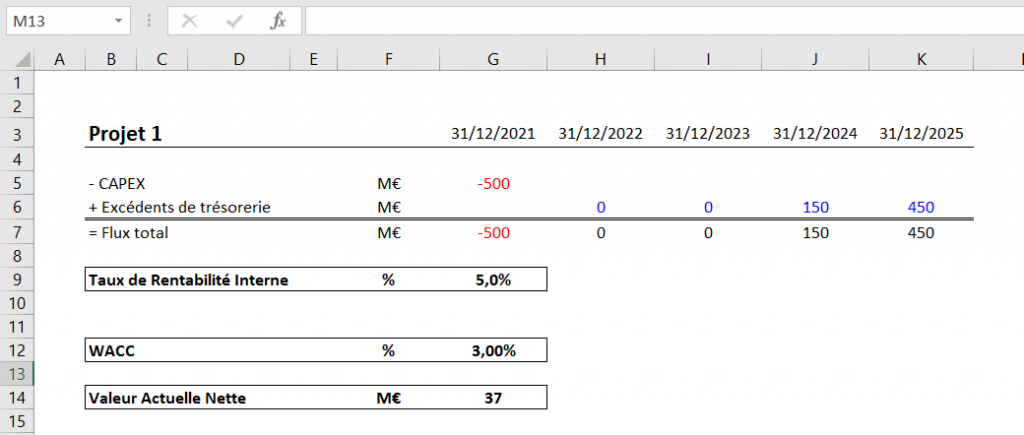
Calcul du TRI et de la VAN du Projet 2
Le projet 2 requiert également un investissement de 500M€ et génèrera, en revanche, 550M€ d’excédents de trésorerie au cours de sa durée de vie. Le TRI est égal à 7.82% et la VAN ressort à 30M€ avec WACC de 3%.
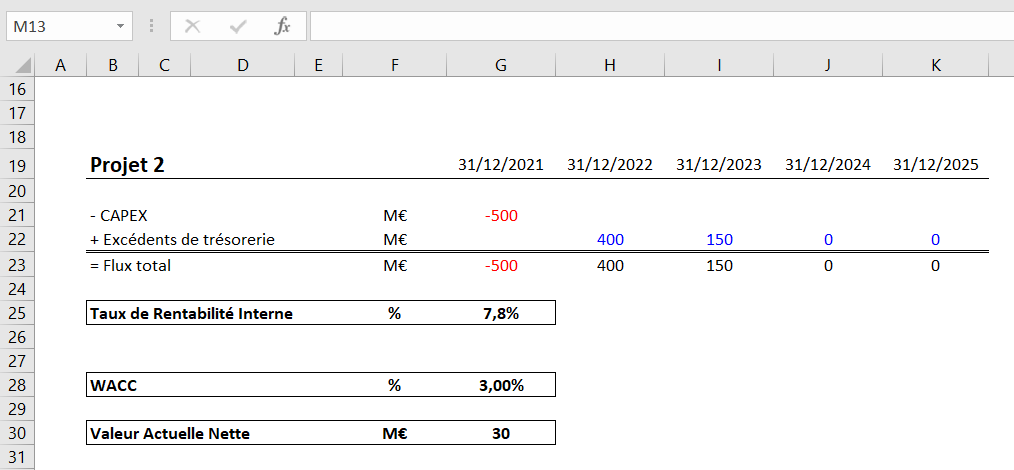
Analyse du calcul du TRI des projets 1 et 2
| Projet 1 | Projet 2 | Avantage | |
| TRI | 4,98% | 7,82% | Projet 2 |
| VAN | 37,05 | 29,74 | Projet 1 |
Comme vous pouvez le constater, le Projet 1 présente un TRI inférieur au Projet 2. Nous serions tentés de conclure qu’investir dans le Projet 2 serait plus intéressant. Cependant, attardons-nous un instant sur la VAN !
La VAN du Projet 1 est supérieure à la VAN du Projet 2 de 7,31M€. Investir dans le Projet 1 nous rapporte 37M€ tandis que le Projet 2 nous rapporte seulement 30M€. Par conséquent, il sera plus intéressant d’investir dans le Projet 1 que dans le Projet 2 (en tout cas, nous préférons personnellement empocher 37M€ plutôt que 30M€ !).
La principale raison est que le Projet 1 génère plus d’excédents de trésorerie en valeur nominale (600M€) que le Projet 2 (550M€). Néanmoins, le Projet 1 perçoit ses flux de trésorerie plus tard dans le temps (en 2024 et 2025), ce qui a pour effet de dégrader son TRI. Alors que le Projet 2 reçoit ses excédents de trésorerie plus tôt dans le temps (en 2022 et 2023), ce qui a pour effet de booster son TRI.
La principale raison de cet écart provient de l’effet temps. En effet, si on nous répète sans cesse que « le temps, c’est de l’argent », ce n’est pas un hasard. Explications dans le chapitre suivant !
La notion de temps dans le calcul TRI
« Time is money » Benjamin Franklin

Cette notion est ultra importante à comprendre si vous souhaitez faire carrière en finance. C’est d’ailleurs cette notion qui explique pourquoi, dans notre exemple précédent, le Projet 2 affiche un TRI plus important que le Projet 1, malgré une VAN inférieure.
En effet, 1€ aujourd’hui n’est pas égal à 1€ demain. Pourquoi me demanderez vous ? Pour plusieurs raisons à vrai dire, et notamment :
- Le risque : par exemple, quelle assurance avez-vous de ne pas vous faire voler cet euro dans le futur ?
- Le manque à gagner : si vous placez 1€ sur un compte épargne, il vous aura rapporter des intérêts et demain vous aurez, par exemple, 1,1€.
- La notion d’utilité (qui symbolise la satisfaction d’un individu) : si cet euro vous permet d’acheter une barre en chocolat, pourquoi attendre demain plutôt que de l’acheter tout de suite ? Si vous attendez demain et que vous acceptez donc de « souffrir » de ce manque de chocolat pendant une journée, c’est en échange de quelque chose ! Vous accepterez donc d’attendre pour obtenir un peu plus d’argent afin de pouvoir acheter un peu plus de chocolat demain plutôt qu’aujourd’hui.
- L’inflation : qui symbolise la hausse constante des prix. A cause de l’inflation, votre barre chocolatée pourrait ne plus coûter 1€ demain mais 2€. Donc votre euro en poche a lui aussi intérêt de s’être transformé en 2€ demain pour pouvoir acheter votre barre chocolatée.
Voilà pourquoi 1€ aujourd’hui vaut plus qu’1€ demain !
Quand une entreprise développe un projet ou fait un investissement, elle doit donc prendre en compte cet effet temps dans ses calculs de rentabilité.
C’est le processus d’actualisation qui permet de prendre en considération l’effet du temps qui passe sur la valeur de l’argent.
En clair, plus le cash-flow est loin de nous dans le temps, plus l’effet d’actualisation va être fort et plus la valeur de ce cash flow futur, ramenée à la date d’aujourd’hui, sera faible.
En revanche, plus le cash-flow est proche de nous dans le temps, plus l’effet d’actualisation va être faible et plus le cash-flow futur aura une valeur proche de sa valeur actuelle.
Vous trouverez, ci-dessous, un exemple afin de vous montrer l’impact de l’effet temps sur l’argent.
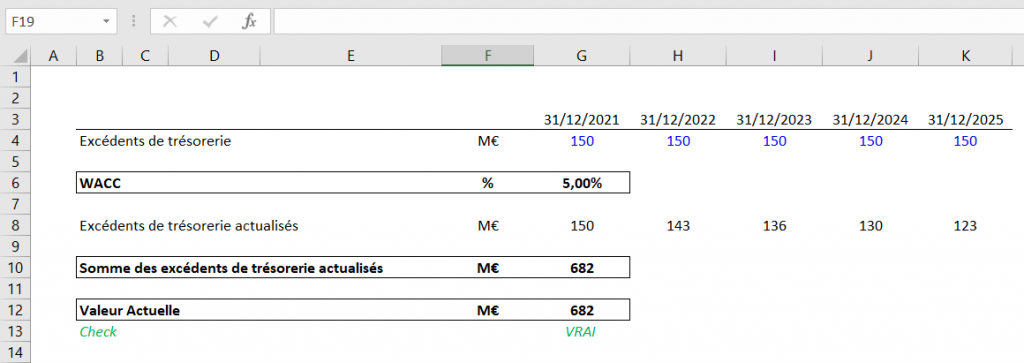
Dans cet exemple, nous avons actualisés un par un les cash-flows perçus de 2021 à 2025. Si nous considérons que nous sommes actuellement en 2020, vous constaterez que le cash-flow 2022 est plus proche de nous dans le temps que le cash-flow 2025. Par conséquent, le cash-flow de 150M€ en 2022 ramené à aujourd’hui (i.e. actualisé) est égal à 143M€ alors que le cash-flow de 150M€ en 2025 ramené à aujourd’hui équivaut à 123M€.
Plus le temps passe, plus l’effet d’actualisation est fort et plus la valeur du cash-flow de base s’effrite. Par conséquent, chaque cash-flow n’a pas le même « poids » dans le temps.
Notez que la somme des excédents de trésorerie actualisés d’un projet représente la Valeur Actuelle (« VA » ou en anglais « Present Value ») de ce projet. La Valeur Actuelle est donc différente de la Valeur Actuelle Nette car elle ne tient pas compte de l’investissement initial.
Dans notre exemple ci-dessus, nous avons additionnés tous les excédents de trésorerie que nous avions, au préalable, actualisés individuellement. Nous avons obtenu la somme de 682M€. C’est une autre manière de calculer la Valeur Actuelle ou la Valeur Actuelle Nette d’un projet. Afin de rassurer notre lecteur sur la justesse de cette méthode, nous avons recalculé la Valeur Actuelle du projet avec la formule VAN.PAIEMENTS et nous obtenons exactement le même résultat ; d’où le Check « Vrai » dans lequel nous avons demandé à Excel si la cellule G12 était bien égale à la cellule G10 (=G12=G10).
NB : dans Excel, vous pouvez calculer une Valeur Actuelle avec la formule VAN.PAIEMENTS. Il suffit simplement de ne pas considérer de cash-flow négatif au début de votre formule.
Nos lecteurs les plus attentifs se demanderont pourquoi, dans notre exemple du chapitre précédent, le Projet 2 génère une VAN moins importante que le Projet 1 alors que ses cash-flows arrivent plus tôt dans le temps. La réponse est simple : c’est la quantité d’argent en valeur nominale qui permet au Projet 1 de dégager une VAN plus importante que le Projet 2. En effet, les excédents de trésorerie du Projet 1 sont estimés à 600M€ alors que ceux du Projet 2 sont estimés à 550M€. Néanmoins, nous pouvons percevoir la puissance de l’effet temps car nous avons une différence de 7M€ entre les 2 VAN alors qu’il y a une différence de 50M€ entre les cash-flows estimés. Cela confirme bien que, plus le cash-flow est loin dans le temps, plus sa valeur actualisée est faible.
Quel indicateur faut-il donc retenir entre le calcul du TRI et la VAN ?
La question est pertinente tant elle fait débat. Certains analystes sont « pro TRI » tandis que d’autres sont « pro VAN ». Nous tâcherons d’apporter un avis neutre afin de ne pas vous influencer. Notez aussi que les conclusions que nous allons tirer sont personnelles et nous supposons que nos lecteurs auront, légitimement, un regard différent du nôtre.
TRI et VAN sont deux indicateurs financiers qui, selon nous, ne peuvent être dissociés lors de la décision d’investissement :
- La VAN permet de déterminer si un projet va créer de l’argent ou en détruire. Cependant, elle n’indique pas si le projet respecte la politique d’investissement de l’entreprise. Dans l’exemple du Projet 1 versus Projet 2 un peu plus haut dans l’article : si le top management de l’entreprise impose une création de valeur de 400bps au-dessus du WACC, cela aboutit à un TRE de 7% (WACC + Création de valeur = 3% + 4% = 7%). Ainsi, l’entreprise n’aurait pas pu investir dans le Projet 1 car le TRI est inférieur au TRE (5% < 7%) quand bien même il dégage une meilleure VAN que le Projet 2 (VAN Projet 1 = 37M€ > VAN Projet 2 = 30M€). En revanche, l’entreprise aurait pu investir dans le Projet 2 qui proposait un TRI supérieur au TRE (7,8% > 7%). Nous comprenons ainsi pourquoi la VAN n’est pas suffisante pour prendre la décision d’investir ou non dans un projet.
- Le TRI permet de déterminer la rentabilité d’un projet et s’il respecte la politique d’investissement de l’entreprise. En revanche, sachez qu’un projet lambda peut présenter un TRI positif et une VAN négative (donc une destruction de valeur !). C’est notamment le cas lorsque le TRI est inférieur au WACC de l’entreprise. C’est la raison pour laquelle une décision d’investissement ne peut pas se baser sur l’unique analyse du TRI.
Exemple ci-dessous avec le Projet 1 où nous supposons que le WACC de l’entreprise est finalement égal à 7%. Le TRI ressort à 5% alors que la VAN est égale à -34M€.
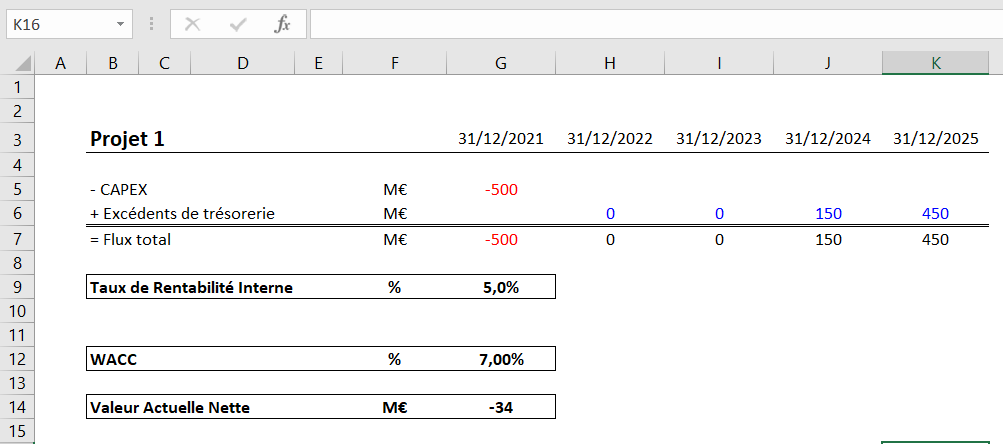
Le TRI dans un contexte macro-économique international changeant
Le Taux de Rendement Interne (TRI) est une mesure clé utilisée en finance pour évaluer la rentabilité d’un investissement. Dans un contexte international, le TRI peut être influencé par une variété de facteurs macroéconomiques, financiers et institutionnels, ce qui nécessite une analyse approfondie pour comprendre ses implications pour les investisseurs étrangers et les multinationales.
Impact des facteurs macroéconomiques et financiers sur le TRI
- Taux d’intérêt : Les taux d’intérêt sont un élément crucial influençant le TRI des investissements. Des taux d’intérêt plus élevés augmentent généralement le coût de financement et réduisent donc le TRI attendu, tandis que des taux d’intérêt plus bas ont tendance à augmenter le TRI en réduisant les coûts d’emprunt.
- Inflation : L’inflation peut également affecter le TRI en impactant la valeur réelle des flux de trésorerie futurs générés par l’investissement. Une inflation élevée peut réduire le pouvoir d’achat des revenus futurs et ainsi réduire le TRI.
- Taux de change : Pour les investissements internationaux, les fluctuations des taux de change peuvent avoir un impact significatif sur le TRI, surtout si les revenus et les coûts sont libellés dans différentes devises. Les mouvements défavorables des taux de change peuvent réduire les rendements attendus et donc le TRI.
Comparaison du TRI des investissements entre pays et secteurs d’activité
- Différences régionales : Le TRI des investissements peut varier considérablement d’un pays à l’autre en raison de différences dans les conditions macroéconomiques, les réglementations gouvernementales, les politiques fiscales et les risques spécifiques au pays. Par exemple, les investissements dans les économies émergentes peuvent offrir des TRI plus élevés mais également être associés à des niveaux de risque plus élevés.
- Secteurs d’activité : Les secteurs d’activité peuvent également avoir des TRI différents en raison de leurs caractéristiques intrinsèques. Par exemple, les industries à forte croissance et à forte technologie peuvent offrir des TRI plus élevés mais également être associées à des niveaux de risque plus élevés par rapport aux secteurs plus stables et matures.
Implications du TRI pour les investisseurs étrangers et les multinationales
- Prise de décision d’investissement : Le TRI est un outil crucial pour les investisseurs étrangers et les multinationales lors de la prise de décisions d’investissement à l’échelle internationale. Il permet de comparer la rentabilité potentielle des investissements dans différents pays et secteurs d’activité et d’identifier les opportunités les plus attractives.
- Gestion des risques : Comprendre les facteurs qui influencent le TRI permet aux investisseurs étrangers et aux multinationales de mieux évaluer et gérer les risques associés à leurs investissements internationaux. Cela peut impliquer la mise en place de stratégies de couverture pour atténuer les risques de change et de diversification pour réduire les risques spécifiques au secteur.
En conclusion, le Taux de Rendement Interne (TRI) dans un contexte international est influencé par une multitude de facteurs macroéconomiques, financiers et institutionnels. Comprendre ces facteurs et leurs implications est crucial pour les investisseurs étrangers et les multinationales afin de prendre des décisions d’investissement éclairées et de gérer efficacement les risques associés à l’investissement à l’échelle mondiale.



 Suivez-nous sur LinkedIn et Instagram pour plus de contenu et conseils :
Suivez-nous sur LinkedIn et Instagram pour plus de contenu et conseils :

