La VAN (« Valeur Actuelle Nette ») est un indicateur financier très important et mondialement reconnu (en anglais, « NPV » ou « Net Present Value ») quand il est question d’analyser la profitabilité d’un projet. Le calcul de la VAN est, par conséquent, une notion incontournable pour celles et ceux qui souhaitent s’orienter vers les métiers de la finance d’entreprise mais également vers les métiers de l’entrepreneuriat ! L’équipe The Big Win a donc décidé de rédiger un article exhaustif sur le calcul de la VAN. C’est dans cet article que vous pourrez trouver définitions, explications, formules, applications, comparaison avec le TRI, etc… Bref, tout ce dont vous avez besoin pour devenir un véritable expert sur le calcul de la VAN. L’aparté sur le TRI peut vous sembler anecdotique alors qu’il n’en est rien. En effet, les notions de calcul de la VAN et du TRI sont absolument indissociables. En clair, si tous ces concepts sont encore un peu flous pour vous, vous êtes tombés au bon endroit et nous vous recommandons vivement la lecture de notre article sur le calcul de la VAN !   

Le calcul de la VAN, qu’est-ce que c’est ?

Concept de base

Lorsqu’il s’agit de développer une entreprise, les projets d’investissement prennent une place prépondérante dans les réflexions liées à la croissance de cette dernière. Pour définir le calcul de la VAN, nous prendrons ici l’exemple d’une entreprise lambda qui décide de créer une nouvelle activité nécessitant la construction d’une nouvelle usine de production. La construction de cet actif impose à l’entreprise d’engager des CAPEX (« Capital Expenditures »), autrement dit des dépenses de constructions. Ces dépenses de constructions seront par la suite contrebalancées par les flux de trésorerie que va générer cette nouvelle usine.

C’est le calcul de la VAN qui va permettre de déterminer si oui ou non, la construction de cette nouvelle usine de production sera bénéfique pour l’entreprise. En effet, dans le calcul de la VAN, nous allons prendre en compte les CAPEX initiaux qui seront considérés comme des flux négatifs et les futurs flux de trésorerie qui seront considérés des flux positifs. De manière imagée, le calcul de la VAN permet de mesurer l’équilibre entre les CAPEX engagés et les futurs flux de trésorerie qui vont être générés par un investissement. Nous reviendrons sur les différentes interprétations de la VAN plus tard dans cet article.  

Notion d’actualisation

Il faut avoir en tête que lorsque nous parlons de Valeur Actuelle Nette, cela implique obligatoirement la notion d’actualisation. En effet, le calcul de VAN implique de ramener les CAPEX et les futurs flux de trésorerie à la date où la VAN est effectivement calculée. Cette action consiste à actualiser un cash-flow, c’est-à-dire à calculer la valeur actuelle d’un cash-flow qui sera perçu dans le futur. Pour actualiser un cash-flow, il faut appliquer un taux d’actualisation. Dans le cadre du calcul de la VAN, nous utilisons principalement le WACC ou le Cost Of Equity en fonction des cash-flows utilisés.

Définition concrète

De manière explicite, la VAN représente la somme des flux actualisés d’un projet. Le calcul de la VAN permet donc de déterminer la totalité de l’argent qui sera générée par un projet auquel nous retranchons son investissement initial (c’est-à-dire ses CAPEX).

Interprétations des résultats du calcul de la VAN

Il faut savoir que lorsque nous calculons une VAN, nous pouvons obtenir différents types de résultats que nous décrivons ci-dessous.

Une VAN négative

Lorsque le calcul de la VAN produit un résultat négatif, cela signifie que les flux actualisés du projet ne sont pas suffisants pour repayer l’investissement initial. La somme des flux actualisés est donc inférieure au montant de CAPEX. En clair, un projet dont la VAN est négative est un projet qui n’est pas rentable dans lequel il ne faut surtout pas investir sous peine de détruire de la valeur.

Exemple : un investissement de 500M€ pour une somme de flux actualisés égale à 450M€ nous donnera une VAN de -50M€.

Une VAN égale à zéro

Lorsque le calcul de la VAN fournit un résultat égal à zéro, cela signifie que les flux actualisés du projet sont suffisants pour récupérer les CAPEX engagés mais pas suffisants pour créer de la valeur pour l’entreprise qui entreprend le projet. Dans ce contexte, la somme des flux actualisés est donc égale au montant de l’investissement initial. Concrètement, d’un point de vue théorique, une VAN égale à zéro représente le point d’équilibre du projet où nous n’enregistrons ni perte, ni bénéfice. Dans la pratique, obtenir une VAN égale à zéro est quasiment impossible tant les facteurs pouvant faire varier le calcul de la VAN sont nombreux.

Exemple : un investissement de 500M€ pour une somme de flux actualisés égale à 500M€ produira une VAN de 0M€.  

Une VAN positive

Lorsque le calcul de la VAN produit un résultat positif, cela signifie que les flux actualisés du projet sont suffisants pour récupérer l’investissement engagé et pour créer une valeur supplémentaire. La somme des flux actualisés est donc supérieure au montant de CAPEX. Par conséquent, nous pouvons dire qu’un projet est rentable à partir du moment où sa VAN est positive et qu’investir dans ce projet permettra à l’entreprise de créer de la valeur.

Exemple : un investissement de 500M€ pour une somme des flux actualisés égale à 550M€ nous permettra d’obtenir une VAN de 50M€.

Calcul de la VAN : les formules à connaitre par cœur

Maintenant que nous avons posé les bases fondamentales du calcul de la VAN, nous pouvons rentrer dans le vif du sujet en communiquant les formules du calcul de la VAN. Pas de formules théoriques ici ! Nous ne présenterons que les utilisations professionnelles de la VAN. Par conséquent, nous n’aborderons que les formules Excel « VAN » et « VAN.PAIEMENTS » dans cet article.

Lorsqu’il s’agit d’effectuer le calcul de la VAN d’un projet, deux composantes doivent être prises en compte : le flux de trésorerie du projet (« cash-flow » en anglais) et le taux d’actualisation à retenir (« discount rate » en anglais).

Les flux de trésorerie

Comme nous l’avons dit précédemment, le calcul de la VAN doit reposer sur un flux de trésorerie. Il faut savoir qu’il existe généralement deux flux de trésorerie sur lesquels peuvent reposer la VAN : le Free Cash-Flow to Firm (« FCFF ») et le Free Cash-Flow to Equity (« FCFE »). Nous rappelons ces deux formules ci-dessous :

Le Free Cash-Flow to Firm représente le flux de trésorerie disponible pour tous les investisseurs et se calcule grâce à la formule suivante :

Free Cash-Flow to Firm = EBIT * (1-tax) + Depreciation & Amortization – Changes in Working Capital – Capital Expenditures

Le Free Cash-Flow to Equity représente le flux de trésorerie disponible uniquement pour les apporteurs de fonds propres :

Free Cash-Flow to Equity = FCFF – Interest Expenses + Capital Increase – Capital Decrease + New borrowings – Debt repayment

Ainsi, lorsque nous calculerons une VAN à partir des Free Cash-Flow to Firm, nous obtiendrons une « VAN Projet », c’est-à-dire une VAN qui reflète la rentabilité pour tous les investisseurs du projet (autrement dit la rentabilité globale du projet).

En revanche, lorsque la VAN est calculée à partir des Free Cash-Flow to Equity, nous obtiendrons une « VAN Equity », c’est-à-dire une VAN qui illustre la rentabilité qui reviendra uniquement aux investisseurs en Equity du projet.  

Les taux d’actualisation

Nous l’avons abordé dans le premier chapitre de cet article, le calcul de la VAN nécessite l’utilisation d’un taux d’actualisation qui diffère en fonction des flux de trésorerie sélectionnés. En clair, lorsque nous calculons une VAN Projet, nous retiendrons le WACC (« Weighted Average Cost of Capital ») comme taux d’actualisation. En revanche, lorsque nous calculons une VAN Equity, c’est le CoE (« Cost of Equity ») qui sera retenu comme taux d’actualisation. Nous effectuons, une nouvelle fois, un rappel des formules ci-dessous :

Le Weighted Average Cost of Capital (ou en Français : Coût Moyen Pondéré du Capital (« CMPC »)) représente le coût pour une entreprise entre ses fonds propres et sa dette, pouvant ainsi correspondre au taux de rentabilité moyen exigé par tous les investisseurs. Il se calcule grâce à la formule ci-dessous :

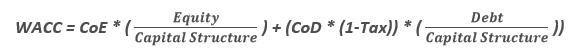
Où :

CoE = Cost of Equity ;

CoD = Cost of Debt ;

1-Tax = Tax Shield ;

Capital Structure = Equity + Debt

Le Cost of Equity représente le taux de rentabilité moyen attendu par tous les investisseurs en fonds propres. Il se calcule grâce à la formule ci-dessous :

Cost of Equity = Risk-Free Rate + Equity Beta * Risk premium

Où :

Risk premium = Total market return – Risk-Free Rate

Formule « VAN » dans Excel

La formule de la VAN est la suivante : 

= VAN (taux ; valeurs)

Où :

Le « taux » est le taux d’actualisation à appliquer (WACC ou CoE) ;

Les « valeurs » sont les flux générés par le projet (FCFF ou FCFE).

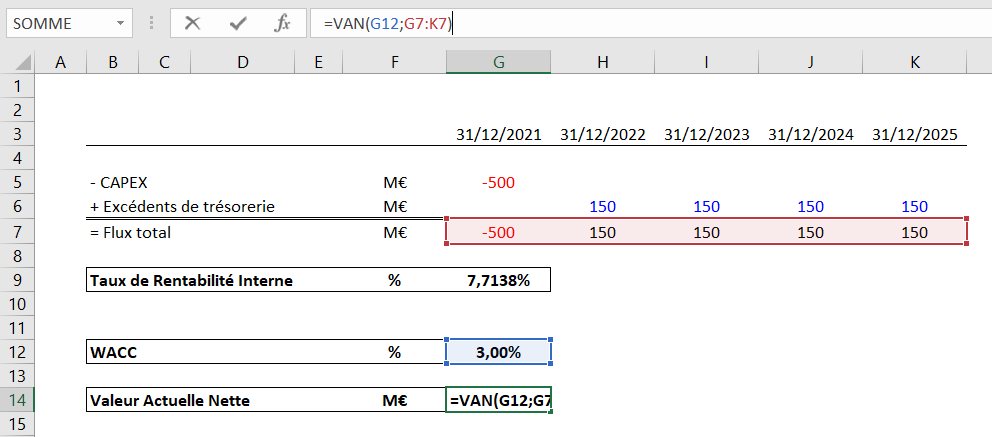
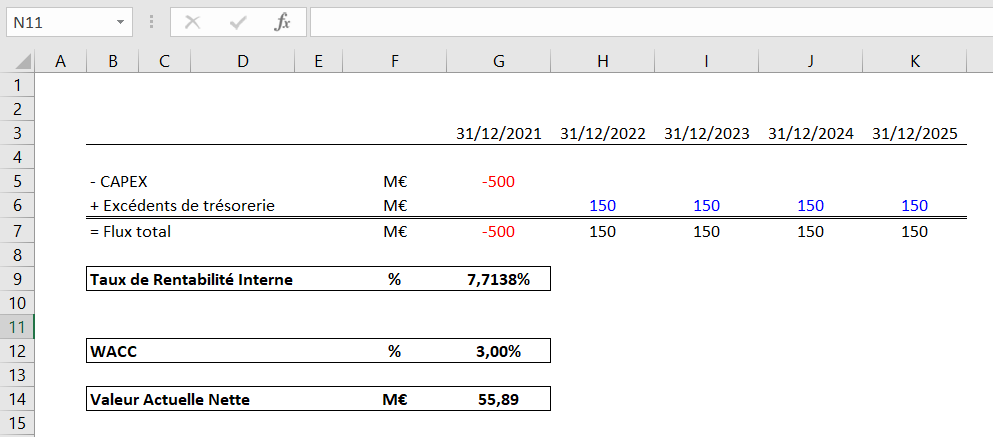
Nous obtenons une VAN de 55,89M€.

Formule « VAN.PAIEMENTS » dans Excel

La formule de la VAN.PAIEMENTS est la suivante :

= VAN.PAIEMENTS (taux ; valeurs ; dates)

Où :

Le « taux » est le taux d’actualisation à appliquer (WACC ou CoE) ;

Les « valeurs » sont les flux générés par le projet (FCFF ou FCFE) ;

Les « dates » sont les dates auxquelles sont générés les flux.

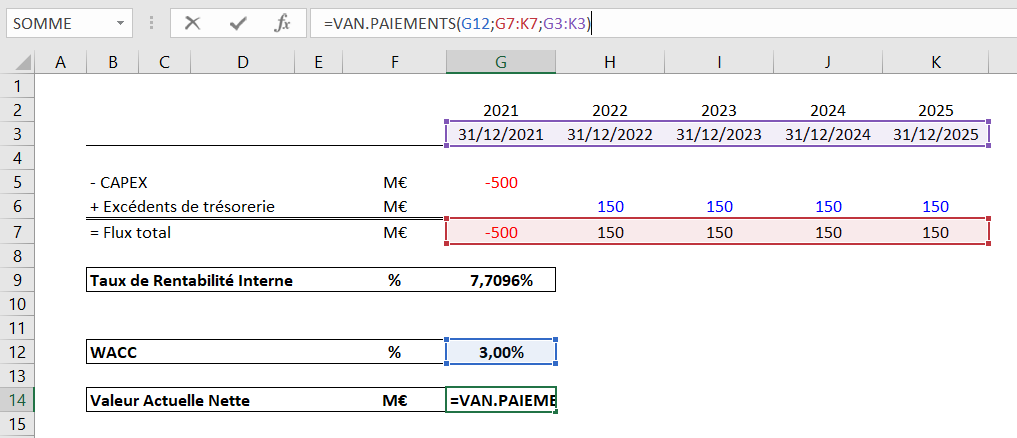
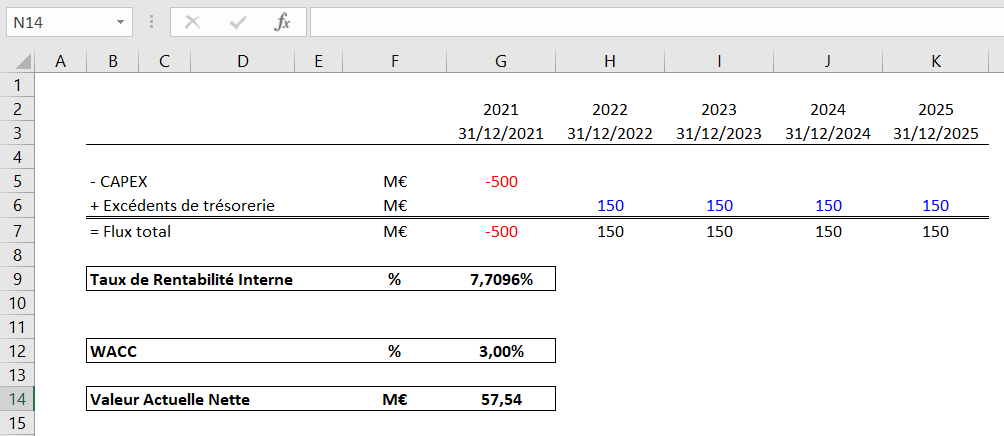
Nous obtenons une VAN de 57,54M€, légèrement supérieure à la VAN que nous avons calculé avec la formule « VAN ». Cette différence provient du fait que la formule VAN.PAIEMENTS est plus précise que la formule VAN car elle prend en compte les dates d’occurrence des cash-flows.

Notez que dans le milieu professionnel, nous recommandons d’utiliser la formule VAN.PAIEMENTS plutôt que la formule de VAN quand il s’agit de réaliser le calcul de la VAN d’un projet.

Le calcul de la VAN vs. le calcul de la VA ?

Dans le monde de la finance, le calcul de la VAN s’oppose au calcul de la VA (« Valeur Actuelle » ou « Present Value » en anglais). Le seul élément qui distingue ces deux indicateurs est l’investissement initial. En effet, dans le calcul de la VA, il n’y a pas de flux de trésorerie négatifs. C’est la raison pour laquelle nous parlons de « Valeur Actuelle » et non de « Valeur Actuelle Nette ». Le calcul de la VA est bien souvent utilisé lorsqu’il s’agit d’estimer la valeur aujourd’hui de revenus perçus dans le futur. Néanmoins, pas d’inquiétudes, la formule du calcul de la VA reste la même que celle utilisée pour le calcul de la VAN, à savoir :  

= VAN (taux ; valeurs)

= VAN.PAIEMENTS (taux ; valeurs ; dates)

Qu’est-ce que le TRI ?

Connaissances élémentaires

Nous ne pouvions faire un article sur le calcul de la VAN sans faire un aparté sur le TRI tant ces deux indicateurs sont indissociables. En effet, lorsqu’il est question d’analyser un investissement, ces deux ratios vont de pair. Pire encore, il y a un véritable débat entre l’utilisation de l’un plus que de l’autre. Nous tâcherons d’apporter quelques éléments de réflexions à ce sujet en fin d’article.

Le TRI (« Taux de Rentabilité Interne » ou « IRR », en anglais pour « Internal Rate of Return ») est un indicateur financier qui permet de mesurer la rentabilité d’un investissement. Comme pour le calcul de la VAN, le TRI va tenir compte de l’investissement initial comme flux négatif et des flux de trésorerie dégagés comme flux positifs. En résumé, le TRI permet de calculer la rentabilité d’un investissement en comparant ses dépenses initiales de CAPEX et les futurs excédents de trésorerie.

Comme pour le calcul de la VAN, le TRI peut être calculé aussi bien à partir du FCFF que du FCFE. Si le TRI est calculé à partir du FCFF, nous parlerons de TRI Projet. A l’inverse, si le TRI est calculé à partir du FCFE, nous parlerons de TRI Equity.

Quel lien entre le calcul de la VAN et le TRI ?

En plus de leur complémentarité, il faut avoir en tête que le calcul de la VAN et celui du TRI sont étroitement liés dans la mesure où le TRI est le taux qui annule la VAN (c’est-à-dire que la VAN est égale à zéro). Nos lecteurs les plus rusés auront compris que pour qu’un projet soit rentable (c’est-à-dire pour qu’il apporte une plus-value, donc une VAN positive), il faut que le TRI soit supérieur au WACC de l’entreprise qui l’entreprends. 

Notion de TRE

Dans le monde de la finance, il ne faut pas confondre TRI et TRE. Le TRE représente le Taux de Rentabilité Exigé (en anglais, le « Required Rate of Return » ou « RRR). En clair, une entreprise n’investira pas dans un projet dont le TRI est inférieur au TRE qu’elle aura fixé. Le TRE est donc un seuil limite en dessous duquel l’entreprise n’investira pas.

Un TRE se calcule à partir du WACC auquel nous ajoutons une marge. De fait, le TRE est constamment supérieur au WACC de l’entreprise. Cette marge s’appelle la « création de valeur ». Il faut également avoir en tête qu’il existe deux types de TRE :

• Le TRI Projet qui se compare au TRE Projet

TRE Projet = Weighted Average Cost of Capital + Création de valeur

• Le TRI Equity qui se compare au TRE Equity

TRE Equity = Cost of Equity + Création de valeur

Petite précision supplémentaire sur la création de valeur : cet indicateur est à la discrétion de chaque entreprise et s’exprimera en pourcentage ou en BPS (prononcé « Bips » et qui signifie « Basis point »).

Les formules du TRI

Nous en profitons pour exposer très rapidement les formules utilisées pour calculer le TRI d’un projet. Pour celles et ceux qui veulent en savoir plus sur le calcul du TRI, nous recommandons vivement la lecture de notre article qui porte à ce sujet, disponible ICI. Comme pour le calcul de la VAN, il existe deux formules Excel pour calculer le TRI d’un projet : la formule « TRI » et la formule « TRI.PAIEMENTS ».

La formule « TRI » sur Excel

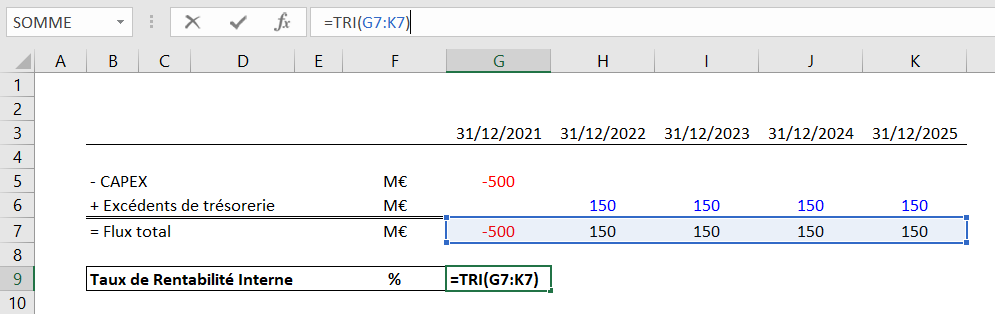
La formule « TRI » est la suivante :

= TRI (valeurs)

Où :

Les « valeurs » sont les flux de trésorerie générés par le projet (FCFF ou FCFE).

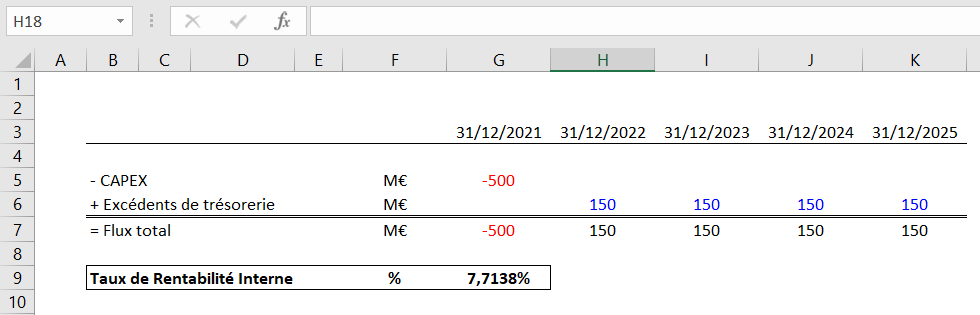
La formule « TRI.PAIEMENTS » sur Excel

La formule « TRI.PAIEMENTS » est la suivante :

= TRI.PAIEMENTS (valeurs ; dates)

Où :

Les « valeurs » sont les flux de trésorerie générés par le projet (FCFF ou FCFE)

Les « dates » sont les dates auxquelles sont générés les flux.

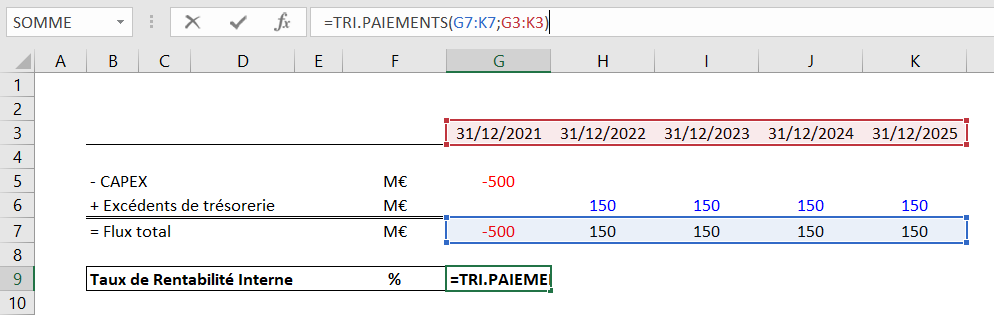
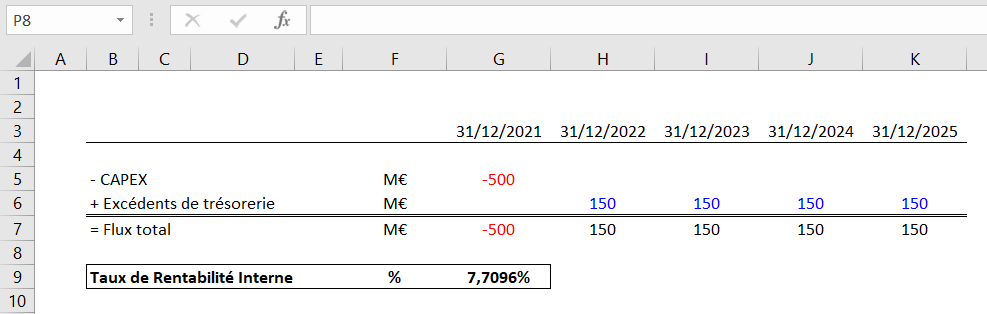
Comme pour le calcul de la VAN, nous observons une différence de résultat entre la formule « TRI » et la formule « TRI.PAIEMENTS » pour la même raison qu’évoquée précédemment, à savoir que la formule « TRI.PAIEMENTS » est plus précise car elle tient compte des dates d’occurrence des flux de trésorerie. C’est la raison pour laquelle, dans un milieu professionnel, nous préférons la formule TRI.PAIEMENTS par rapport à la formule du TRI classique.

Le TRI annule le calcul de la VAN

Dans ce chapitre, nous allons vous démontrer comment le TRI annule le calcul de la VAN. Nous reprenons notre exemple ci-dessus où :

• TRI = 7,7096%
• WACC = 3,00%
• VAN = 57,54M€

Pourquoi le calcul de la VAN est positif ?

Pour répondre à cette question, il faut bien comprendre la relation qui existe entre TRI, WACC et calcul de la VAN. Dans notre exemple, le calcul de la VAN donne un résultat positif car le TRI du projet (7,7096%) est largement supérieur au WACC de notre entreprise (3,00%). Pour savoir si un projet lui sera bénéfique, une entreprise va réaliser son calcul de la VAN en utilisant son propre WACC comme taux d’actualisation.

En clair, l’idée est de déterminer si la création de valeur apportée par un projet va être suffisante pour satisfaire la rentabilité des actionnaires. Dans notre exemple, la réponse est oui car l’entreprise espère une rentabilité d’au moins 3,00% tandis que le projet permet d’atteindre une rentabilité de 7,71%.

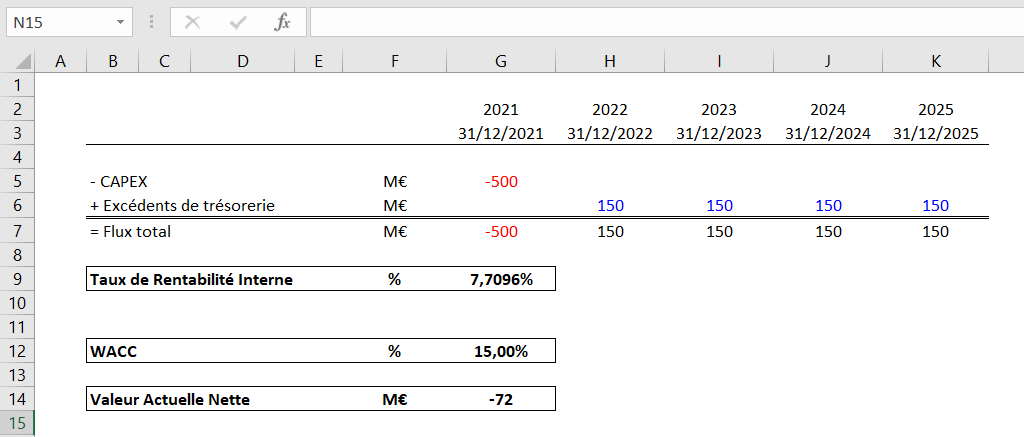
Comment le calcul de la VAN aurait pu donner un résultat négatif ?

Si le WACC de l’entreprise avait été égal à 15%, alors le projet n’aurait pas apporté la rentabilité nécessaire pour créer une plus-value à l’entreprise. Le calcul de la VAN aurait donc été négatif. Nous pouvons conclure que lorsque le TRI d’un projet est inférieur au WACC de l’entreprise, alors le calcul de la VAN fournira toujours un résultat négatif.

Comment le calcul de la VAN aurait pu donner un résultat neutre ?

En revanche, si le WACC de l’entreprise avait été de 7,71%, le calcul de la VAN aurait donné un résultat égal à zéro car le projet aurait apporté exactement la rentabilité que l’entreprise attendait. C’est la raison pour laquelle nous disons sans cesse que le TRI est le taux d’actualisation qui annule la VAN.

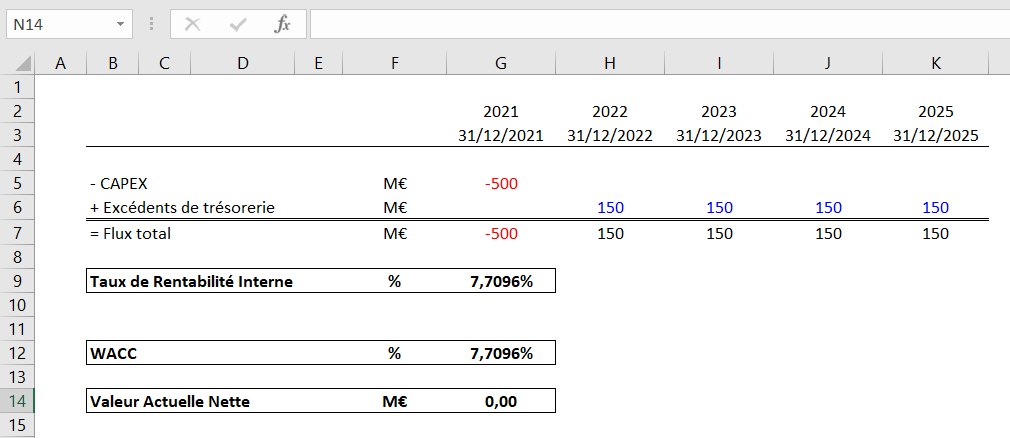
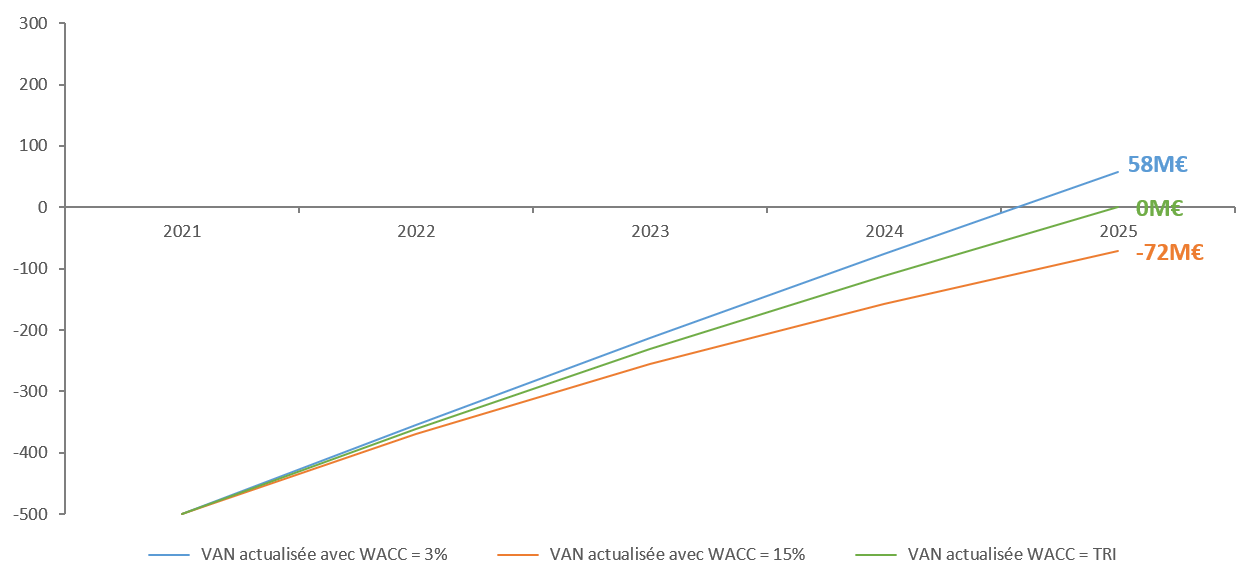
Illustration de tous les résultats

Afin de vous proposer une image concrète et simple à retenir, nous avons réalisé le graphique ci-dessous qui regroupe tous les calculs de VAN que nous avons présenté dans ce chapitre.

Calcul de la VAN : faut-il toujours investir dans un projet dont le TRI est le plus élevé ?

Pour répondre à cette question, nous prenons l’exemple de deux projets : le projet 1 qui affiche un TRI de 5% et le projet 2 qui affiche, quant à lui, un TRI de 8%. Aux premiers abords, il nous semblerait évident d’investir directement dans le projet 2 car il présente un TRI supérieur. Néanmoins, le calcul de la VAN joue un rôle très important et nous allons vous le démontrer dans ce chapitre. Dans les exemples suivants, nous supposerons un WACC de 3%.

Calcul de la VAN du projet 1

Le projet 1 suppose des CAPEX à hauteur de 500 millions d’euros pour une somme de flux de trésorerie égale à 600 millions d’euros. Nous calculons un TRI d’environ 5% et une VAN de 37 millions d’euros en utilisant un WACC de 3%.

Calcul de la VAN du projet 2

Dans le second projet, nous supposons également des CAPEX de 500 millions d’euros. Cependant, ici, la somme des flux de trésorerie sera égale à 550 millions d’euros. Avec ces hypothèses, le projet 2 affiche un TRI de 7,8% et une VAN de 30 millions d’euros en utilisant le même WACC de 3%.

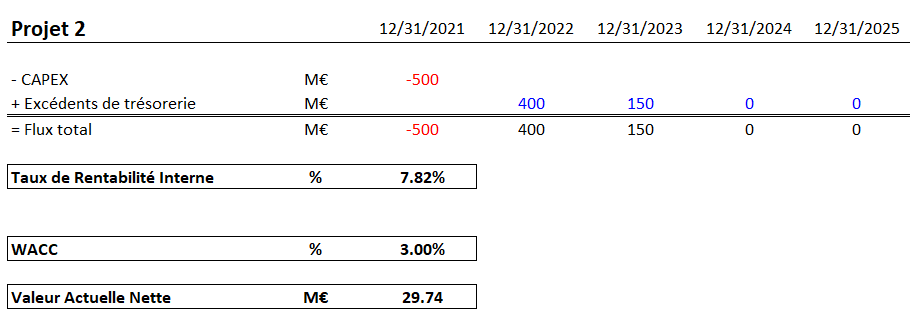
Analyse des résultats

Comme nous l’avons dit au début de ce chapitre, le projet 2 semble plus intéressant que le projet 1 car il présente un TRI beaucoup plus intéressant. Néanmoins, le calcul de la VAN prend toute son importance ici car il nous montre que le projet 2 créé moins de valeur que le projet 1 (30M€ < 37M€). D’un point de vue VAN, le projet 1 est donc beaucoup plus intéressant que le projet 2 (du moins, nous préférons personnellement recevoir 37M€ plutôt que 30M€).

La principale raison de ces différences est que le projet 1 génère plus de flux de trésorerie en valeur nominale (600M€) que le projet 2 (550M€). Néanmoins, comme le projet 1 reçoit ses flux de trésorerie plus tard dans le temps, cela a tendance à dégrader son TRI. A l’inverse du projet 2 qui reçoit ses flux de trésorerie tout de suite, ce qui aura tendance à booster son TRI.

Au travers de cette analyse, nous percevons bien l’impact de l’effet temps sur l’argent. Plus un flux de trésorerie est lointain moins il aura de valeur aujourd’hui. Ce n’est pas un hasard si tout le monde répète, depuis des décennies, que « le temps, c’est de l’argent ».

Quel indicateur faut-il donc retenir entre le calcul de la VAN et du TRI ?

Eternel débat dans le monde de la finance : faut-il opter pour le TRI ou la VAN lorsqu’il s’agit d’analyser la rentabilité d’un projet. Bien évidemment, la réponse est propre à chacun et selon nous, il n’y a pas de bonne ou de mauvaise réponse. Par ailleurs, il nous semble toujours pertinent de ne pas focaliser une décision d’investissement sur l’analyse d’un seul indicateur financier. Bref, nous tâcherons d’apporter un avis neutre sur la question dans cet ultime article afin de ne pas vous influencer.

Selon nous, VAN et TRI sont deux indicateurs financiers complémentaires qui ne peuvent pas être séparés lors d’une décision d’investir. En effet, chacun de ces indicateurs apportent des informations cruciales que nous exposons ci-dessous :

La VAN indique la création de valeur

Comme nous l’avons répété à maintes reprises dans cet article, le calcul de la VAN permet de déterminer si un projet est capable de créer de l’argent ou non. Néanmoins, la VAN n’indique pas si le projet respecte la politique d’investissement de l’entreprise. Dans l’exemple du Projet 1 versus le Projet 2 du chapitre précédent, si l’entreprise impose une création de valeur de 400bps, le TRE à respecter aurait été égale à 7,0%. L’entreprise n’aurait donc pas investi dans le projet 1 car il n’aurait pas permis de respecter ce TRE (5,0% < 7,0%) quand bien même il présente un calcul de la VAN beaucoup plus favorable. L’entreprise se serait donc tournée vers le projet 2 qui présentait une rentabilité beaucoup plus satisfaisante d’un point de vue TRE (7,8% > 7,0%). Cet exemple démontre bien pourquoi le calcul de la VAN n’est pas suffisant pour prendre une décision d’investissement.

Le TRI indique la rentabilité

Dans cette ultime partie, nous reprenons les mêmes bases que dans le chapitre précédent à savoir qu’un TRI élevé n’est pas toujours synonyme de VAN élevée. Pour être beaucoup plus extrême, il faut avoir en tête qu’un projet peut présenter, conjointement, un TRI positif et une VAN négative. Cela est rendu possible lorsque le TRI d’un projet est inférieur au WACC de l’entreprise. Vous comprenez donc pourquoi une décision d’investissement ne peut reposer sur la seule analyse du TRI d’un projet.