En finance, le calcul de taux est une tâche fondamentale, et par extension, le calcul de taux composés annuels (aussi abrégé en “CAGR”, prononcé “Cagar”) l’est aussi.  

Que ce soit pour calculer un taux de croissance de revenus, un taux de croissance de la valeur d’un actif ou toute autre évolution dans le temps, chaque financier doit maîtriser ces notions sur le bout des doigts. 

Dans cet article, nous allons vous expliquer tout ce que vous devez savoir sur la notion et les formules de CAGR, le contexte dans lequel l’utiliser et les erreurs à éviter. 

Calcul du CAGR : définition 

CAGR est l’acronyme de Compouned Annual Growth Rate, que l’on peut traduire en français par Taux de Croissance Annuel Composé. 

Le CAGR correspond au taux de croissance annuel moyen sur une période donnée. 

Il permet ainsi d’établir quel taux de croissance annuel moyen serait équivalent à plusieurs taux intermédiaires répartis sur plusieurs années. 

Ainsi, imaginons l’évolution du chiffre d’affaires d’une entreprise qui augmenterait de 15% la première année, diminuerait de -3% l’année suivante et réaugmenterait de 20% la troisième année.  

Dans ce cas, le calcul du CAGR permet d’établir quel taux de croissance annuel fixe pendant 3 ans serait équivalent à ces trois taux différents consécutifs. 

Le calcul du CAGR simplifie donc énormément la lecture du taux de croissance d’une métrique dans le temps, que ce soit un chiffre d’affaires, la rentabilité d’une action, ou tout autre taux, notamment pour faire des comparaisons entre plusieurs actifs ou plusieurs entreprises. 

En effet, si vous devez comparer la croissance du chiffre d’affaires de deux entreprises, A et B, sur trois ans, avec les taux suivants : 

Entreprise A : +10% en année 1, +7% en année 2, -3% en année 3 

Entreprise B : +15% en année 1, -5% en année 2, +2% en année 3 

Vous risquez d’avoir beaucoup de mal à répondre instinctivement laquelle de ces deux entreprises a le mieux performé sur cette période totale de 3 ans.  

En revanche, si nous faisons le calcul du CAGR du chiffre d’affaires de ces deux entreprises sur 3 ans, vous aurez alors : 

Entreprise A : CAGR de 4,5% sur 3 ans, ce qui signifie qu’une croissance fixe de +4,5% par an pendant trois ans correspond exactement à des taux consécutifs de +10%, +7% et –3%. 

Entreprise B : CAGR de 3,7% sur 3 ans, ce qui signifie qu’une croissance fixe de +3,7% par an pendant trois ans correspond exactement à des taux consécutifs de +15%, -5% et +2%. 

Dans cet exemple, on peut répondre facilement que c’est l’entreprise A qui a connu la croissance la plus importante sur ces trois dernières années puisque le calcul du CAGR indique un taux de croissance moyen de 4,5%, supérieur au CAGR de 3,7% de l’entreprise B. 

Calcul du CAGR : la formule 

Calcul du CAGR à la main 

Maintenant que nous avons vu sa définition et son utilité, il reste à voir quelle formule utiliser pour faire un calcul de CAGR.  

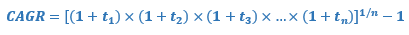
Ce qui peut aussi s’écrire avec l’opérateur de produit : 

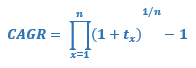
Avec : 

• tn = le taux de croissance en période n 
• n = le nombre de périodes sur lesquelles on veut faire notre calcul de CAGR 

Voici un exemple de calcul de CAGR. 

Nous souhaitons calculer le taux de croissance moyen d’une entreprise sur 3 ans, qui a présenté successivement la croissance moyenne de chiffre d’affaires suivante : 

• Année 1 : +5% 
• Année 2 : +8% 
• Année 3 : -2% 

Si nous appliquons la formule que nous venons de voir pour le calcul du CAGR de cette société, nous avons l’équation suivante : 

Ce calcul de CAGR nous permet donc de constater que les taux de croissance, année après année, de cette entreprise correspondent à un taux de croissance annuel fixe de 3,6% en moyenne. 

Attention, il est aussi possible, et même parfois nécessaire, de calculer un CAGR non pas à partir de taux de croissance individuels, mais à partir d’une valeur monétaire de départ et de fin. 

Dans ce cas, la formule est la suivante :

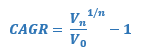
Avec : 

• V0 = la valeur en période 0 
• Vn = la valeur en période n 
• n = le nombre de périodes totale 

Afin d’illustrer cette formule, nous reprenons notre exemple précédent et nous considérons que l’entreprise pour laquelle nous voulons réaliser un calcul de CAGR sur le chiffre d’affaires présente les chiffres d’affaires suivants : 

• Année 0 : 100 € 
• Année 1 : 105 € (soit 5% de croissance par rapport à l’année 0) 
• Année 2 : 113 € (soit 8% de croissance par rapport à l’année 1) 
• Année 3 : 111 € (soit -2% de croissance par rapport à l’année 2) 

Alors le calcul du CAGR est le suivant : 

Comme vous pouvez le constater, notre résultat est strictement identique au calcul de CAGR précédent qui utilisait les taux : 3,6% en moyenne. 

Calcul du CAGR sur Excel 

Dans le milieu professionnel, vous serez très certainement amené à réaliser le calcul de CAGR non pas “à la main” mais bien sur Excel derrière un écran. 

Voyons donc comment procéder dans ce cas. 

Sur Excel, il n’existe malheureusement pas de formule pour faire un calcul de CAGR directement à partir de plusieurs taux. En revanche, vous pouvez utiliser la formule de moyenne géométrique à condition de faire manuellement les “+1” à chaque taux annuel et le “–1” au résultat final. 

Voici le même exemple que précédemment pour éclaircir les choses : 

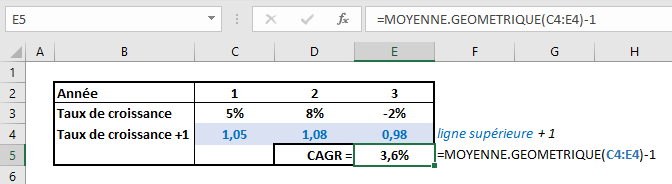
Dans la première ligne du tableau, nous avons la liste des croissances du chiffre d’affaires de l’entreprise chaque année.  

Dans la seconde ligne, nous ajoutons simplement +1 à chacun de ces taux de croissance. 

Pour réaliser notre calcul de CAGR, il ne nous reste plus qu’à utiliser la formule MOYENNE.GEOMETRIQUE à cette deuxième ligne puis de retirer 1 au résultat final. Nous obtenons bel et bien un CAGR de 3,6% similaire à notre calcul réalisé précédemment à la main. 

Concernant le calcul de CAGR sur Excel à partir de valeurs de départ et d’arrivée en euros, le processus est plus simple car vous n’avez pas besoin d’étape intermédiaire comme avec les taux auxquels vous devez ajouter +1.  

En effet, dans le cas de valeurs monétaires, il vous suffit d’utiliser la formule : 

=TAUX.INT.EQUIV(npm;va;vc) 

Avec : 

• npm = la période maximale
• va = la valeur monétaire de départ 
• vc = la valeur monétaire de fin 

Si l’on continue d’utiliser le même exemple, cela nous donne le tableau ci-dessous : 

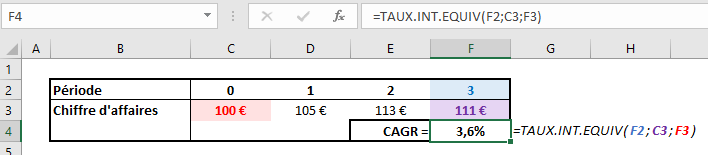
On retrouve encore un résultat final de 3,6% pour notre calcul de CAGR. 

Comprendre le CAGR comparé à une moyenne simple 

Maintenant que vous maitrisez parfaitement la définition et les formules du calcul de CAGR, il faut faire attention à ne pas tout mélanger car lorsqu’on l’on parle de moyenne, les erreurs arrivent en général très vite. 

Ainsi, il ne faut surtout pas mélanger le CAGR, qui est un taux moyen, avec un taux de croissance simple. Si vous avez du mal à cerner la différence avec cette simple phrase, ne vous inquiétez pas, nous allons préciser cette subtilité. 

Si nous reprenons notre exemple précédent, le chiffre d’affaires de l’entreprise à la fin de la dernière année est de 111€, tandis qu’il était de 100€ en début de première année. 

La principale erreur serait ainsi de confondre le CAGR et le taux de croissance simple sur cette période : 

• Le taux de croissance simple est : (111 € / 100€) – 1 = 11%. 
• Le CAGR est de 3,6%, comme nous l’avons calculé à plusieurs reprises précédemment. 

En fait, les deux taux signifient en pratiquent la même chose, mais l’expriment de manière différente. 

Le taux de croissance simple ignore toute notion de durée ou de période : on calcule simplement la croissance entre le point de départ (100€) et d’arrivée (111€). 

Le calcul de CAGR indique quant à lui le taux de croissance nécessaire sur chaque période pour passer du point de départ (100€) au point d’arrivée (111€) si l’on découpe cette durée totale en un nombre identique de périodes. En l’occurrence, ici, une période correspond à un an et la durée totale au passage du début de l’année 0 à la fin de l’année 3. 

On pourrait donc résumer en disant qu’une croissance de 3,6% par an entre l’année 0 et l’année 3 aboutit à une croissance totale de 11% sur cette période. 

Les limites du CAGR 

Le CAGR n’est pas représentatif des taux de croissance intermédiaires réels 

La principale limite du calcul de CAGR est qu’il ignore totalement les valeurs réelles de la donnée que l’on suit entre le point de départ et le point d’arrivée. Si l’on reprend notre exemple, voici un rappel de la croissance du chiffre d’affaires de notre entreprise année après année : 

• Année 1 : +5% 
• Année 2 : +8% 
• Année 3 : -2% 
• CAGR = 3,6% 

On constate ainsi qu’en année 3, elle a subi une diminution de son chiffre d’affaires. Or cela est impossible à deviner si l’on vous donne simplement le CAGR de 3,6%.  

En fait, il s’agit ici du même risque que lorsqu’on travaille avec des moyennes : si lors d’un contrôle de géographie, la moyenne d’une classe est de 14/20, il est tout à fait possible qu’il y ait des écarts importants, avec des élèves qui auront 19/20 et d’autres qui auront 5/20. 

Lorsque vous faites un calcul de CAGR, vous devez donc toujours avoir en tête que c’est un calcul de moyenne qui n’est pas égal aux taux de croissance réels, année après année. 

Le CAGR ne donne pas d’indication sur la volatilité du taux de croissance 

La deuxième limite du CAGR est en fait une prolongation de la première : c’est le fait qu’en plus de ne pas être représentatif des taux intermédiaires réel, il ne donne pas d’indication sur la volatilité du taux de croissance.  

Ainsi, il est tout à fait possible d’avoir, pour deux CAGR égaux tous deux calculés sur des séries de taux de croissance très différents. 

Voici un exemple pour illustrer cela. 

Imaginons, non plus deux entreprises, mais deux actions cotées en bourses pour lesquelles nous souhaitons calculer un taux de rentabilité moyen grâce à un calcul de CAGR : 

Comme vous pouvez le constater, le calcul de CAGR de ces deux actions entre l’année 0 et l’année 3 donne le même résultat, à savoir 2%. 

Pourtant ces deux actions n’ont pas du tout la même volatilité : l’action A affiche une volatilité faible avec des taux de croissance qui restent compris entre +5% et –2%. 

L’action B, quant à elle, souffre d’une volatilité très forte puisqu’elle varie entre +16% et –20%. 

En finance, cela peut avoir une grande importance, car la notion de risque est cruciale et le risque est lui-même mesuré par la volatilité. Dans certains cas, vous voudrez à tout prix éviter des écarts aussi importants que ceux de l’action B alors même que finalement sa croissance moyenne est similaire à celle de l’action A. 

Quand utiliser le calcul du CAGR 

Le CAGR est très pratique tout d’abord pour comparer la croissance de deux entreprises ou deux actifs différents, comme nous vous le montrions en début d’article. 

En effet, si on vous propose des séries de croissances annuelles pour plusieurs investissements différents, vous aurez forcément du mal à définir lequel est le meilleur d’un coup d’œil. 

Le CAGR règle ce problème en proposant une croissance moyenne unique facile à comparer. 

Si nous reprenons l’exemple précédent de nos deux actions, il est impossible, en un coup d’oeil, de dire quelle action entre la A et la B représente le meilleur investissement. Ce n’est qu’en faisant un calcul de CAGR que l’on remarque qu’avec une croissance moyenne de 2% chacune, elles affichent en fait une rentabilité strictement similaire sur la période qui nous intéresse. 

Le deuxième cas où l’utilisation du CAGR est pratique est pour comparer des croissances sur des durée différentes. Seul le CAGR nous permet de faire ça car on calcule une moyenne annuelle. 

Voici un exemple pour être plus précis. Imaginons deux action, X et Y, pour lesquelles nous souhaitons comparer la croissance. Seulement nous avons un problème, l’action Y est côtée en bourse depuis 5 ans alors que l’action X n’a été introduite en bourse que depuis 3 ans. Pour pouvoir comparer les résultats historiques de ces deux actions, on peut donc procéder à un calcul de CAGR qui nous donnera une moyenne annuelle pour chacune : 

Si l’on fait un calcul de CAGR pour établir la croissance moyenne des deux actions depuis qu’elles sont cotées en bourse, soit 3 ans pour X et 5 ans pour Y, on peut donc voir que c’est X qui a été la plus rentable. 

Enfin, attention avec ces calculs sur des durées différentes tout de même qui peuvent induire en erreur et doivent être manipulés avec attention, car l’action Y a pu subir une crise qu’a évité l’action X car elle n’était pas encore cotée. Par exemple, en année 1, on voit qu’Y a subi une chute de -4% alors que X n’avait pas encore de donnée disponible à ce moment là. Vous devez donc vous assurer qu’aucun élément extérieur ne vient désavantager une action par rapport à l’autre.