Le modèle Black Scholes est l’un des outils les plus connus qui permet, en théorie, de calculer le prix d’une option de type européenne en fonction de différentes données de cette option et de l’actif sous-jacent sur lequel elle est adossée.

Le modèle Black Scholes peut parfois faire peur à des juniors et étudiants alors que finalement, il est assez simple d’utilisation.

Enfin, c’est un concept crucial à maîtriser puisqu’il est relativement fréquent d’avoir des questions à son sujet lors d’entretiens sur des postes qui touchent de près ou de loin à la gestion d’actifs. Dans cet article, nous vous expliquons tout ce que vous devez savoir sur le modèle Black Scholes simplement et efficacement.

Modèle Black Scholes : définition

Le modèle Black Scholes est un modèle mathématique d’évaluation du prix d’une option de type européenne qui permet d’estimer sa valeur théorique en fonction de ses caractéristiques et des caractéristiques du sous-jacent sur lequel elle porte.

Le modèle Black Scholes est donc avant tout une formule mathématique dont la première publication date de 1973 par Robert Merton sur la base de travaux de Fischer Black et de Myron Scholes. Cela vaudra d’ailleurs à Merton et Scholes le prix Nobel d’économie en 1997 (Fischer Black, qui est décédé en 1995, avant la remise de ce prix, a été cité comme contributeur).

La grande innovation du modèle Black Scholes est de faire largement intervenir la variation de prix de l’actif sous-jacent dans le calcul de la valeur de l’option.

Explication sur l’utilisation de modèle Black Scholes

Maintenant que nous avons défini ce qu’est le modèle Black Scholes, il est nécessaire d’aller plus loin afin de comprendre concrètement à quoi sert cet outil et parce que chez The Big Win, notre objectif est de vous apporter des informations financières concrètes, exhaustives et pratiques que vous ne trouverez pas ailleurs.

Pour aller plus loin, il est nécessaire de maîtriser quelques notions financières utilisées par le modèle Black Scholes :

Qu’est-ce qu’une option ?

Une option en finance est un produit dérivé sur action (equity derivatives en anglais), c’est-à-dire un contrat passé entre deux opérateurs de marché et qui repose sur la transaction d’un actif sous-jacent (la plupart du temps une action, une obligation, une devise ou un taux).

Il existe deux grands types d’options : les calls et les puts

Un call est une option qui donne le droit à celui qui la détient d’acheter l’actif sous-jacent à la contrepartie de l’option à un prix fixé à l’avance pendant un laps de temps donné.

Par exemple, imaginons que vous étudiez l’action de l’entreprise fictive The Big Win Corp. Elle cote actuellement 100€ sur les marchés boursiers. Vous pensez que son prix va monter d’ici 6 mois mais vous ne souhaitez pas mobiliser 100€ pour l’acheter aujourd’hui afin de la revendre plus tard. A la place, vous pouvez donc acheter une option call dont l’actif sous-jacent est l’action The Big Win. Vous achetez cette action pour 5€ et elle vous permet, si vous l’exercez, d’acheter l’option The Big Win au prix de 102€ dans 6 mois. Finalement, 6 mois plus tard, le prix de l’action The Big Win a augmenté à 120€. Vous décidez donc d’exercer votre option qui vous donne le droit d’acheter l’action The Big Win à 102€, auprès de la personne qui vous a vendu l’option. Il vous suffit ensuite de la revendre à 120€ sur les marchés pour faire un profit de 120 – 5 – 102 = 13€ pour un investissement initial de 5€ seulement.

L’option put donne le droit à celui qui la détient de vendre l’actif sous-jacent à la contrepartie de l’option à un prix fixé à l’avance pendant un laps de temps donné.

Imaginons, maintenant que vous êtes le PDG de The Big Win Corp. Au titre de votre rémunération variable, vous obtenez 1000 actions de l’entreprise que vous avez l’interdiction de vendre pendant 1 an sachant qu’elles cotent maintenant 120€. Si vous avez peur que le cours baisse d’ici 1 an, alors vous pouvez souscrire à des options puts qui vous permettront de vendre dans 1 an vos actions au prix de 118€. Si dans 1 an, le prix de l’action a chuté à 90€ alors vos options puts vous permettront de les vendre malgré tout au prix de 118€. Inversement, si le prix de l’action a augmenté à 130€ alors vous laisserez expirer vos options et vous aurez perdu le prix que vous avez mis pour les acheter.

Quelle est la différence entre une option européenne et une option américaine

L’option dite européenne est une option qui donne le droit à son détenteur de l’exercer uniquement à sa date d’échéance. Une option américaine est une option que vous pouvez exercer à n’importe quel moment entre la date à laquelle elle est émise et sa date d’expiration. Ainsi, imaginons deux options, une européenne et une américaine, toutes deux émises le 1 janvier 2020 avec une date d’expiration au 31 décembre 2020. L’option européenne ne peut être exercée que le 31 décembre 2020 alors que l’option américaine peut être exercée à n’importe quel moment de l’année 2020. Etant donné que l’option américaine peut être exercée pendant un laps de temps plus long, elle est vendue plus cher que l’option américaine. Le modèle Black Scholes permet d’évaluer les options européennes.

Quelle est la différence entre prix et valeur ?

Là, c’est une distinction que peu de personnes font et qui est pourtant primordiale : le prix n’est pas la valeur et réciproquement. Il est important d’en parler car le modèle Black Scholes permet d’estimer la valeur d’une option, qui peut différer de son prix. Le prix est le montant que vous devez mettre sur la table pour acquérir un actif ou une option. Sa valeur est généralement définie comme le prix maximum qu’un acteur est prêt à payer pour acquérir un actif. Si le prix est inférieur à la valeur que vous estimez, cela signifie que vous devez investir dans l’actif. Le modèle Black Scholes permet d’estimer la VALEUR d’une option, qui peut donc différer de son prix sur les marchés. Ceci-dit, l’objectif d’un marché financier efficient est de rapprocher le plus possible le prix de la valeur, donc de calculer la valeur d’un actif ou d’une option et de définir son prix de manière égale à sa valeur.

Utilité concrète du modèle Black Scholes

Maintenant que nous avons vu ces notions primordiales à la compréhension du modèle Black Scholes, nous pouvons voir à quoi il sert concrètement.

Comme nous l’avons vu dans nos exemples précédents, une option, call ou put, n’est pas gratuite, elle s’achète. Toute la question est donc d’estimer un prix égal à sa valeur que l’on peut évaluer notamment grâce au modèle Black Scholes.

Ainsi, le modèle Black Scholes servira concrètement à deux types d’opérateurs de marché :

• L’émetteur (ou vendeur) de l’option : il peut se servir du modèle Black Scholes pour savoir à quel prix émettre ou vendre une option en fonction des caractéristiques de l’option qu’il va émettre et de l’actif sous-jacent.
• L’acheteur de l’option : pour savoir quelle est la valeur d’une option et donc à quel prix maximum il devrait l’acheter.

Surtout, ce qu’il faut voir c’est que la valeur, donc le prix d’une option, varie tout au long de sa vie.

Si nous reprenons notre exemple initial de l’action The Big Win corp qui cote à 100€ et que vous avez acheté une option call à 5€ pour l’acheter 102€ dans 6 mois. Nous imaginons que, cinq mois plus tard, le prix de l’action The Big Win a déjà augmenté à 115€. Vous vous doutez bien que si vous décidez non pas d’attendre encore un mois pour exercer votre option call mais plutôt de la vendre immédiatement alors vous la vendrez plus cher que le prix auquel vous l’avez acheté.

Vous ne la vendrez alors plus 5€ mais 13€, ce qui correspond à la différence de prix entre le prix d’exercice de l’option (102€) et le prix actuel de l’action sous-jacente (115€). En effet, la vendre moins cher serait synonyme de perdre la plus-value évidente permise par votre option, et la vendre plus cher n’aurait aucun intérêt pour l’acheteur potentiel.

Cet exemple permet d’illustrer que la valeur et le prix d’une option évoluent continuellement au cours de la vie d’une option, ce qui accentue encore le modèle Black Scholes.

Modèle Black Scholes : formules et calculs de ce modèle financier

Maintenant que nous avons vu la définition et l’intérêt d’utiliser le modèle Black Scholes, voyons sa formule :

Modèle Black Scholes pour l’évaluation d’une option Call

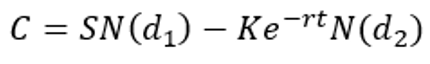
où :

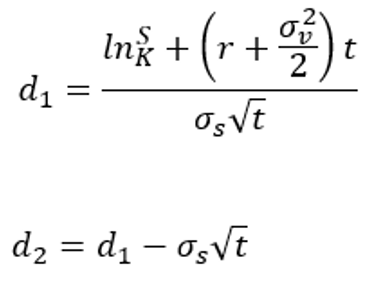
et :

C = la valeur de l’option call

S = le prix actuel de l’action sous-jacente

K = le prix de l’exercice de l’option, appelé « Strike Price »

r = le taux sans risque

t = le temps restant jusqu’à la date d’exercice de l’option (en année)

N = la fonction de répartition de la loi normale centrée réduite N(0,1)

σ = la volatilité du prix de l’action sous-jacente

Modèle Black Scholes pour l’évaluation d’une option Put

De même, il est possible d’utiliser une autre variante du modèle Black Scholes pour évaluer, non pas une option call, mais une option put. La formule put est alors :

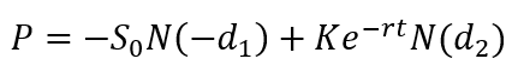
où :

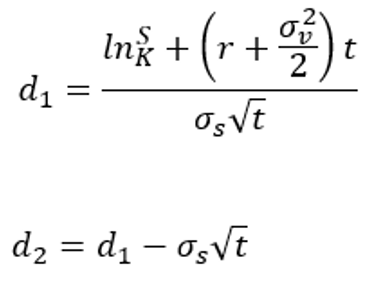
et :

P = la valeur de l’option put

S = le prix actuel de l’action sous-jacente

K = le prix de l’exercice de l’option, appelé « Strike Price »

r = le taux sans risque

t = le temps restant jusqu’à la date d’exercice de l’option (en année)

N = la fonction de répartition de la loi normale centrée réduite N(0,1)

σ = la volatilité du prix de l’action sous-jacente

Comment utiliser le modèle Black Scholes

Il est nécessaire de donner quelques précisions d’ordre pratique pour utiliser le modèle Black Scholes au vu de la complexité des formules que nous venons de vous exposer.

Plus particulièrement, nous voulons donner des précisions sur les termes N(d1), N(d2) et N(-d1) qui sont souvent ceux sur lesquels la plupart des juniors et étudiants bloquent.

En fait, le N signifie l’utilisation de la loi normale centrée réduit N(0,1). Il s’agit donc dans un premier temps de calculer les termes d1 et d2 avec les deux sous-formules que nous vous avons indiquées. Une fois que vous avez ces deux termes, il suffit alors de chercher leur correspondance dans la table de la loi normale centrée réduite N(0,1) :

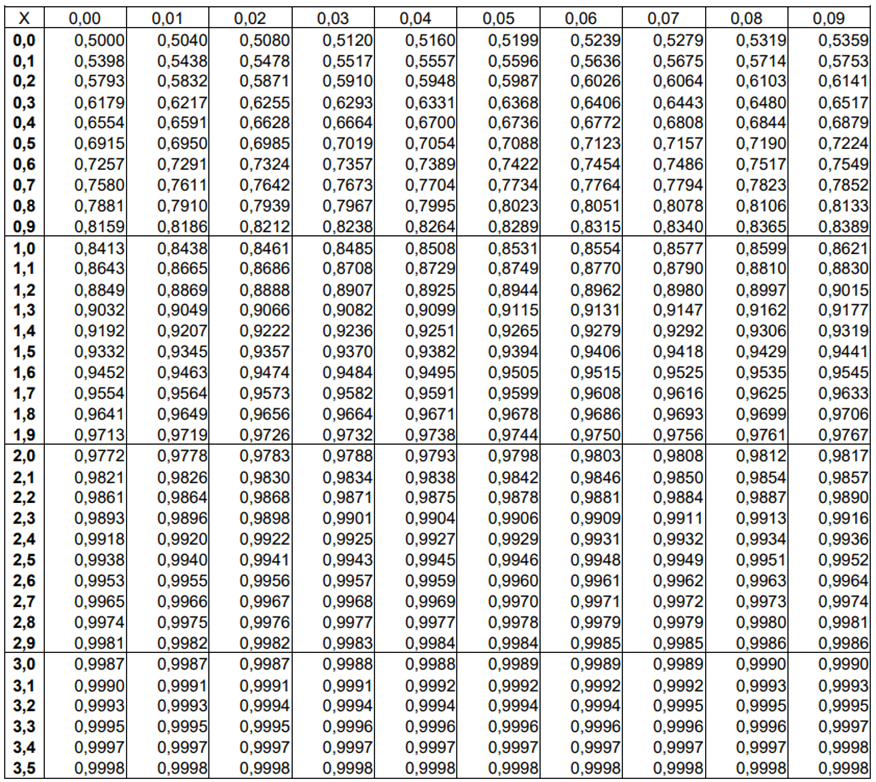
Pour utiliser cette table, il faut chercher la correspondance de votre d1 et d2 en cherchant leur unité et première décimale sur l’axe des ordonnées et leur deuxième décimale sur l’axe des abscisses.

Par exemple, si votre calcul de d1 donne un résultat de 0,53 alors la valeur N(d1) sera 0,7019 que l’on trouve au croisement de la ligne 0,5 et de la colonne 0,03.

Attention, si d1 ou d2 sont négatifs alors vous devrez retrancher le résultat de votre table à 1. Pour être plus clair, imaginons maintenant que votre calcul de d1 donne pour résultat -0,35 alors vous devez d’abord chercher la correspondance de 0,35 (valeur positive) dans la table, soit 0,6368 mais cette fois, pour N(d1), vous devez retenir 1 – 0,6368 soit 0,3632.

Modèle Black Scholes : exemple d’utilisation

Exemple d’utilisation du modèle Black Scholes pour l’évaluation d’un call

Imaginons que vous vouliez émettre un call sur les marchés avec pour sous-jacent l’action de l’entreprise The Big Win Corp. La maturité du call émis est de 1 semestre (6 mois) et le strike price de 110€ sachant que l’action cote actuellement à 102€. Le taux sans risque est de 2% et vous calculez une volatilité du prix de l’action The Big Win Corp de 42%.

Nos hypothèses (ou inputs dans le jargon) sont donc les suivantes :

S = 102

K = 110

r = 2%

t = 0,5 (puisqu’un semestre correspond à 0,5 an)

σ = 42%

Il convient tout d’abord de calculer d1 et d2 :

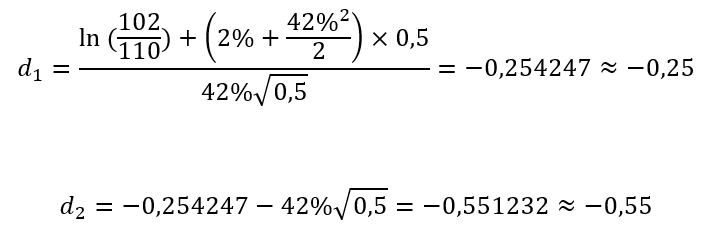
L’étape suivante consiste à chercher les correspondances des valeurs absolues de d1 et d2 dans la table de la loi normale, et étant donné que d1 et d2 sont négatifs, de retrancher à 1 les valeurs que l’on trouvera :

• La valeur absolue de d1 est 0,25. La valeur correspondante dans la table est 0,5987 (ligne 0,2 et colonne 0,05). Etant donné que d1 = -025 (et non 0,25) alors N(d1) = 1-0,5987 = 0,4013
• La valeur absolue de d2 est 0,55. La valeur correspondante dans la table est 0,7088 (ligne 0,5 et colonne 0,05). Encore une fois, d2 étant négatif (-0,55 et non 0,55), il faut prendre N(d2) = 1-0,7088 = 0,2912

Enfin, nous pouvons maintenant appliquer le modèle Black Scholes :

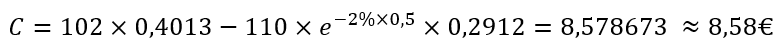
Nous avons donc calculé que cette option Call doit être proposée au prix de 8,58€.

Exemple d’utilisation du modèle Black Scholes pour l’évaluation d’un put

Imaginons maintenant que vous souhaitiez émettre un Put avec pour sous-jacent l’action The Small Win Corp. La maturité du put émis est de 1 trimestre (3 mois) et le strike price de 40€ sachant que l’action cote actuellement à 43€. Le taux sans risque est toujours de 2% et vous calculez une volatilité du prix de l’action The Small Win Corp de 64%.

Nos inputs sont donc les suivants :

S = 43

K = 40

r = 2%

t = 0,25 (puisqu’un trimestre correspond à 0,25 an)

σ = 64%

Comme précédemment, nous calculons d’abord d1 et d2 :

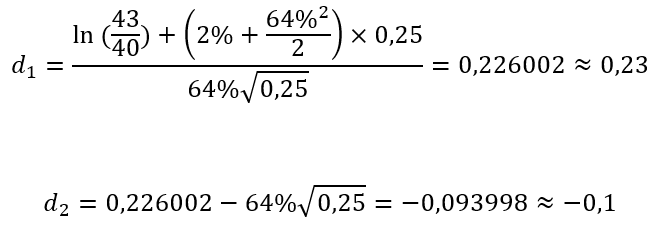
Ensuite, il faut chercher les correspondances de -d1 et d2 dans la table :

• N(-d1) = 1-0,5910 = 0,4090
• N(d2) = 1-0,5398 = 0,4602

Et nous pouvons ensuite appliquer le modèle Black Scholes :

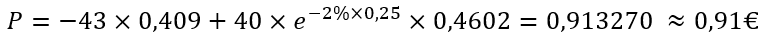
Nous avons donc calculé une valeur de 0,91€ pour ce put trimestriel grâce au modèle Black Scholes

Les limites du modèles Black Scholes

Différents économistes et intellectuels ont remis en question la robustesse du modèle Black Scholes, au premier rang desquels le mathématicien Benoît Mandelbrot.

La principale critique qui est faite de cette méthode est sa supposée déconnexion de la réalité des marchés financiers. Le modèle, bien que brillamment construit, serait « trop théorique ».

Cette déconnexion serait surtout la conséquence de l’utilisation de la loi normale. En effet, cette loi a le mérite de très bien fonctionner dans un environnement « normal », mais elle prédit très mal les évènements extrêmes. Par conséquent, le modèle Black Scholes serait incapable de s’adapter à des environnements très rares mais qui existent pourtant bel et bien comme les krachs boursiers.

En bref, le modèle est mathématiquement cohérent, logique, compréhensible et facilement utilisable mais il simplifie beaucoup trop la réalité et prend des hypothèses trop théoriques et utopistes comme la notion de rationalité parfaite des investisseurs.

Malgré ces critiques, il reste le modèle le plus utilisé pour valoriser des options et c’est la technique de référence qu’apprend tout bon étudiant en finance.

Vous savez maintenant tout ce qu’il y a à savoir sur le modèle Black Scholes, n’hésitez pas à nous dire ce que vous en pensez et si vous avez aussi eu l’occasion de l’utiliser dans votre carrière ou vos études.