Les mathématiques financières sont une matière incontournable pour quiconque envisage un cursus universitaire en finance. Vous l’avez compris, si vous envisagez de faire une carrière en finance, vous serez obligés de passer par la case mathématiques financières. Et quand bien même vous ne souhaitez pas travailler dans le monde de la finance, il faut savoir que c’est une matière qui est généralement étudiée lors des années en tronc commun dans la plupart des grandes écoles de commerce.
De par son intitulé, les mathématiques financières peuvent effrayer ceux qui ne sont pas spécialement à l’aise avec les mathématiques en général. C’est à ce moment que The Big Win se doit d’intervenir. En effet, les mathématiques financières ne sont pas une matière foncièrement difficile à partir du moment où cette dernière est enseignée de manière claire. La raison est simple : les mathématiques financières ne sont que l’application bête et méchante de formules pour réaliser des calculs et / ou résoudre des problèmes. Encore faut-il comprendre à quoi servent ces formules.
L’équipe The Big Win a décidé de rédiger un article complet sur les mathématiques financières afin de proposer une vision simple et concise d’une matière qui ne doit plus être crainte par les étudiants, quelque soit la formation suivie. Dans cet article, vous retrouverez les notions élémentaires expliquées de manière à ce qu’elles soient compréhensibles de tous. En d’autres termes, c’est grâce à cet article que vous comprendrez les tenants et les aboutissants des mathématiques financières.
- Que sont les mathématiques financières ?
- Mathématiques financières : la différence entre un prêt et un emprunt
- Les différentes composantes en mathématiques financières
- Mathématiques financières : notions d’actualisation et de capitalisation
- Mathématiques financières : notions d’intérêts simples et d’intérêts composés
- Mathématiques financières : notions d’annuités
- Les mathématiques financières sont-elles difficiles à appréhender ?
- L’importance des mathématiques financières
- Exemples concrets d’application de mathématiques financières
- Les mathématiques financières : quelles études ?
- Dans quels métiers de la finance retrouve-t-on les concepts liés aux mathématiques financières ?

Que sont les mathématiques financières ?
Les mathématiques financières sont une composante des mathématiques appliquées. La particularité des mathématiques financières est, comme son nom l’indique, qu’elles s’appliquent aux opérations financières.
Comme vous le savez déjà tous, une citation très célèbre de Benjamin Franklin reflète parfaitement le fondement même des mathématiques financières : le temps, c’est de l’argent. En effet, les mathématiques financières ont pour caractéristique de prendre en compte le temps qui passe, impliquant ainsi certains concepts incontournables en finance tels que l’actualisation et la capitalisation.
Ainsi, les mathématiques financières vont nous permettre de calculer, avec précision, des intérêts issus d’opérations financières. Il existe, en règle générale, deux grands types d’opérations financières dans les mathématiques financières qui sont le placement et l’emprunt. Nous reviendrons sur ces sujets un peu plus tard dans l’article.
En clair, les mathématiques financières permettent de déterminer combien nous coûte l’argent que nous empruntons ou encore combien va nous rapporter un placement quelconque.
Afin de fournir un premier exemple concret à notre lecteur, c’est grâce aux mathématiques financières qu’une banque calcule la somme que vous devez rembourser lors d’un prêt immobilier.
Mathématiques financières : la différence entre un prêt et un emprunt
En mathématiques financières, il est important de bien comprendre la subtilité entre un prêt et un emprunt car comme nous l’avons dit, il existe deux grands types d’opérations financières.
Le prêt consiste à prêter notre argent à quelqu’un moyennant une rémunération : le taux d’intérêt. Cette personne s’engage à nous rembourser la somme d’argent que nous lui avons prêtée en plus de nous payer des intérêts. Concrètement, lorsqu’une banque vous prête de l’argent, elle réalise un prêt. Dans la même optique, lorsque vous placez votre argent sur un livret quelconque, vous prêtez votre argent à la banque.
L’emprunt consiste à emprunter de l’argent à quelqu’un moyennant une rémunération : encore une fois, le taux d’intérêt. L’emprunt est tout simplement le pendant du prêt. Lorsque vous prêtez de l’argent à quelqu’un, vous êtes le prêteur et cette personne est l’emprunteur. Lorsqu’une banque vous accorde un prêt, vous avez le statut d’emprunteur.
Pour résumé, le prêteur prête une somme d’argent à un emprunteur et l’emprunteur rembourse cette somme d’argent au bout d’un certain laps de temps en plus de payer des intérêts.
Les différentes composantes en mathématiques financières
En mathématiques financières, lorsqu’il est question de placement ou d’emprunt, il est important de distinguer plusieurs notions essentielles que nous récapitulons ci-dessous :
Le nominal en mathématiques financières
Le nominal d’un prêt ou d’un emprunt est simplement le montant de ce dernier. En d’autres termes, c’est le montant d’argent que vous souhaitez emprunter ou placer. Le nominal peut être exprimé de différentes manières comme par exemple le principal, le montant ou le capital.
Le taux d’intérêts
Le taux d’intérêts est le taux grâce auquel nous calculons les intérêts d’un prêt ou d’un placement. Il s’applique au nominal d’un prêt et doit être adaptée à la période d’intérêts de l’opération financière. En résumé, le taux d’intérêts n’est autre que la rémunération d’une opération financière qui revient à la personne qui accepte de prêter son argent.
De manière concrète, lorsqu’une banque accorde un prêt immobilier, sa rémunération est le taux d’intérêts car, à la fin du prêt, vous lui aurez remboursé le nominal du prêt, ce qui représentera une opération neutre pour elle (elle vous a prêté 200 000€ en année N, vous lui rendez 200 000€ en année N+20 c’est-à-dire au bout de 20 ans). En revanche, sur ces 20 années, vous aurez payé tous les mois des intérêts qui ont été calculés grâce au taux d’intérêts. Ainsi, sur cette opération financière, la banque gagnera de l’argent grâce aux intérêts que vous lui verserez.
Le calcul d’intérêts en mathématiques financières
Les intérêts sont, comme nous l’avons indiqué précédemment, l’argent que vous payerez à l’organisme qui vous prête une somme d’argent ou l’argent que vous recevrez d’un placement financier. Il faut garder en tête que le taux d’intérêts est un pourcentage qui s’applique au nominal du prêt pour déterminer les intérêts de ce dernier.
La durée du prêt
La durée du prêt est, comme son nom l’indique, la durée sur laquelle le prêt s’étend.
La période de capitalisation
La période de capitalisation est la période de calcul des intérêts. En d’autres termes, c’est le rythme auquel les intérêts vont être payés. De manière générale, en mathématiques financières, nous distinguons quatre période de capitalisation : mensuelle, trimestrielle, semestrielle et annuelle.
A titre d’exemple, un prêt de 20 ans, remboursable mensuellement aura une durée de 20 ans et une période de capitalisation mensuelle.
Mathématiques financières : notions d’actualisation et de capitalisation
En mathématiques financières, et plus généralement en finance, il existe deux grands concepts incontournables lorsqu’il est question d’estimer la valeur de l’argent dans le temps : l’actualisation et la capitalisation.
Car oui, 1 euro aujourd’hui n’a pas la même valeur dans 10 ans. Il peut se passer tellement d’évènements en 10 ans que nous n’avons aucune garantie que cet euro aujourd’hui vaudra toujours 1 euro dans 10 ans. Pour prendre en compte ces risques, nous devons effectuer des calculs qui permettent de prendre en compte cette notion de temps qui passe. C’est pour cela que nous devons actualiser ou capitaliser en fonction des situations.
L’actualisation en mathématiques financières
Le principe d’actualisation a pour objectif de déterminer la valeur de l’argent aujourd’hui alors qu’elle sera perçue dans le futur.
Lorsque vous souhaitez réaliser un investissement, votre objectif est de déterminer s’il sera rentable ou non en perspective des flux de trésorerie futurs qu’il pourra vous rapporter. Votre but est donc de ramener la valeur de ces flux que vous percevrez plus tard, à la date d’aujourd’hui pour déterminer si votre investissement sera rentable ou non.
La capitalisation
Le principe de capitalisation est tout simplement l’inverse du principe d’actualisation. Il permet donc d’estimer la valeur qu’aura l’argent dans le futur.
C’est exactement ce qu’il se passe lorsque vous allez demander un emprunt à votre banque. Cette dernière va estimer les intérêts que vous devrez payer dans le futur. Elle calcule aujourd’hui, la valeur qu’ils auront plus tard dans le futur.
Pour éviter toute confusion, nous proposons un schéma récapitulatif ci-dessous :
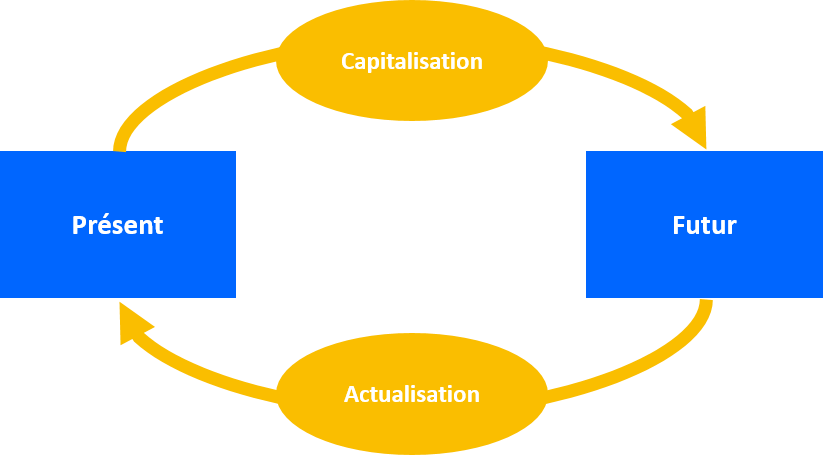
Attention, il est également important de faire la distinction entre le principe de capitalisation et la capitalisation des intérêts qui sont deux notions différentes. En effet, la capitalisation des intérêts consiste à ajouter, au nominal, les intérêts de la période précédente afin que la base de calcul des intérêts de la période suivante soit plus élevée. Nous reviendrons sur ce point dans le chapitre suivant, mais ce processus permet aux intérêts de générer plus d’intérêts.
Mathématiques financières : notions d’intérêts simples et d’intérêts composés
En mathématiques financières, il existe deux types d’intérêts : les intérêts simples et les intérêts composés. Il est important de bien faire la distinction entre ces deux nuances clefs.
Les intérêts simples
Les intérêts sont définis comme « simples » lorsque la période de calcul (c’est-à-dire la période d’intérêts) est proportionnelle à la durée du prêt. En mathématiques financières, les intérêts simples sont les plus faciles à calculer car il suffit simplement d’appliquer le taux d’intérêt au montant du prêt. Par conséquent, les intérêts doivent être payés uniquement à la fin de l’opération financière.
En d’autres termes, les intérêts sont simples lorsque la période de capitalisation des intérêts est égale à la durée du prêt.
Les intérêts composés
Les intérêts sont définis comme « composés » à partir du moment où les intérêts sont ajoutés au montant du principal de l’emprunt / placement à chaque période de capitalisation et qui sert ensuite de nouvelle base de calcul pour les intérêts suivants.
En d’autres termes, les intérêts doivent être composés lorsque la période de capitalisation des intérêts est inférieure à la durée du prêt. Cela veut donc dire que les intérêts doivent être calculés et payés plus d’une fois lors de la durée du prêt. A titre d’exemple : un prêt de 12 ans dont les remboursements sont annuels imposera de calculer 12 fois les intérêts.
Mathématiques financières : notions d’annuités
En mathématiques financières, il est également très important d’aborder la notion d’annuités. Les annuités représentent des versements effectués à intervalles constants. De manière concrète, ce sont toutes les échéances qui peuvent exister entre la valeur actuelle (c’est à dire la valeur de l’argent que nous empruntons / plaçons aujourd’hui) et la valeur future (c’est à dire la valeur de l’argent que nous remboursons / récupérerons dans le futur).
- Lorsque les intérêts sont simples : dans un prêt dont les intérêts sont simples, il existe qu’une seule annuité puisque, comme nous l’avons dit précédemment, les intérêts sont payés à la fin de l’opération.
- Lorsque les intérêts sont composés : dans un prêt dont les intérêts sont composés, il existe plusieurs annuités avec des intérêts non payés qui s’ajoutent au principal du prêt au fur et à mesure des annuités.
Pour être plus précis, nous parlons de :
- Annuités quand la période de capitalisation des intérêts est annuelle
- Semestrialités quand la période de capitalisation des intérêts est semestrielle
- Trimestrialités quand la période de capitalisation des intérêts est trimestrielle
- Mensualités quand la période de capitalisation des intérêts est mensuelle
Les mathématiques financières sont-elles difficiles à appréhender ?
La réponse est NON à partir du moment où les grandes notions sont parfaitement comprises et maitrisées et que les formules sont connues sur le bout des doigts. Il existe également certaines subtilités à maitriser comme par exemple l’équivalence des taux.
L’apprentissage efficace des mathématiques financières passent, avant tout, par la réalisation d’exercices. En effet, c’est en exerçant et en se trompant que nous pouvons percevoir et comprendre toutes ces petites subtilités qui font la différence !
Les mathématiques financières ne sont finalement que l’application de formules classiques pour répondre à des problématiques concrètes. Qui plus est, il existe certaines astuces pratiques et simples à mettre en place pour vérifier ses propres résultats.
Pour celles et ceux qui veulent aller plus loin dans l’apprentissage des mathématiques financières, nous proposons des fiches synthétiques qui reprennent toutes les notions élémentaires à connaitre sur cette matière, toutes les formules importantes, toutes nos astuces pour réussir ses calculs à coup sûr mais aussi des dizaines d’exercices pour pouvoir s’entrainer et mettre en application les concepts abordés.
=> CLIQUEZ ICI POUR ACCÉDER A NOS FICHES DE RÉVISIONS SUR LES MATHÉMATIQUES FINANCIÈRE <=
L’importance des mathématiques financières
Les mathématiques financières sont une matière très importante car elles permettent de comprendre avec précision les opérations financières que nous rencontrerons forcément, un jour ou l’autre, dans notre quotidien. D’où l’importance d’avoir, à minima, quelques notions pour savoir de quoi il est question ! Dans le chapitre suivant, nous fournissons des exemples concrets dans lesquels les mathématiques financières sont utilisées !
Au-delà de votre quotidien personnel, ce sont également des calculs auxquels vous aurez affaire lors de votre quotidien professionnel dans le monde de la finance. Nous l’aborderons plus tard dans l’article, mais les concepts abordés dans les mathématiques financières se retrouvent dans énormément de métiers financiers, d’où l’importance de maitriser sur le bout des doigts cette matière. Même si vous ne serez peut-être pas la personne qui réalise tous ces calculs, vous serez forcement confrontés un jour ou l’autre à ces calculs et concepts.
Exemples concrets d’application de mathématiques financières
Afin de parfaire la culture de notre lecteur, il nous semble indispensable de présenter des exemples concrets dans lesquels nous retrouvons l’application des mathématiques financières. Nous dressons donc ci-dessous, une liste non exhaustive d’exemples d’application des mathématiques financières :
- Le calcul des intérêts de placements bancaires : Livret A, Livret Jeune, Livret d’Epargne Populaire ou encore Livret de Développement Durable et Solidaire
- Le calcul des intérêts d’une assurance vie
- Le calcul des intérêts d’un emprunt bancaire : prêt immobilier, prêt à la consommation, prêt relais, prêt d’acquisition quelconque (exemple : voiture).
- Le calcul des intérêts d’un leasing
- Le calcul des intérêts d’une obligation financière
Les mathématiques financières : quelles études ?
La question que vous pouvez légitimement vous poser est la suivante : dans quelles études vais-je rencontrer les mathématiques financières ? C’est la question à laquelle nous répondons dans ce chapitre :
- Ecole de commerce : Il faut savoir que la matière mathématiques financières sont présentes dans tous les cursus en tronc commun des écoles de commerce. C’est un passage obligatoire auquel vous ne pourrez pas échapper avant de vous spécialiser.
- Universités : dans les cursus universitaires, en fonction de votre spécialisation, vous pourrez être amenés à rencontrer les mathématiques financières. Nous pensons particulièrement au cursus en finance évidemment, mais également en assurance, en banque, en économie ou encore en gestion.
- BAC + 2 : les mathématiques financières sont abordées dans très peu de formation BAC +2 de par son caractère très spécifique et de sa difficulté. Néanmoins, vous les rencontrerez à coup sûr en DUT GEA (Gestion des Entreprises et des Administrations) par exemple, ou encore dans les classes préparatoires aux grandes écoles, voie technologique.
De manière générale, les mathématiques financières sont une matière systématiquement abordée dans les formations qui touchent de près ou de loin aux mathématiques appliquées, à la finance, à l’assurance ou à la gestion d’entreprise.
Dans quels métiers de la finance retrouve-t-on les concepts liés aux mathématiques financières ?
La réponse est : dans la majorité des métiers du monde de la finance. Dans ce dernier chapitre, nous citons, de manière non exhaustive, quelques exemples de métiers dans lesquels il est important de connaitre les mathématiques financières et ses concepts. Notez que nous essayons de proposer une vision très générale car il ne faut pas oublier qu’aucun métier n’est similaire et, par extension, chaque métier dispose de spécificités qui lui sont propres.
- Analyste financier : en tant qu’analyste financier, vous pourrez être amenés à analyser des offres de prêts reçues par votre entreprise (quel que soit sa taille) pour réaliser tel ou tel projet. Votre rôle sera donc de vérifier et de comprendre les calculs réalisés par l’organisme bancaire proposant le ou les prêts en question.
- Analyste investissement : en tant qu’analyste investissement, votre rôle sera de comprendre toutes les notions liées à l’actualisation pour déterminer si oui ou non, il est rentable d’effectuer tel ou tel investissement ou tel ou tel placement.
- Analyste M&A : tout comme l’analyste investissement, l’analyste M&A sera également confrontés aux thématiques d’actualisation et à la notion de « temps qui passe ». Qui plus est, il aura pour rôle de concevoir le business plan financier pour déterminer la faisabilité financière de telle ou telle opération et d’en estimer les impacts. D’où l’importance d’être à l’aise avec la notion d’actualisation et d’intérêts.
- Analyste financement de projet : l’analyste financement de projet devra également avoir en tête toutes les notions abordées dans les mathématiques financières. En effet, son rôle sera de modéliser dans un business plan le financement de tel ou tel projet. Il sera donc régulièrement en contact avec les banques et devra comprendre la documentation bancaire. En effet, il sera responsable de la bonne compréhension des informations à intégrer dans le modèle financier pour obtenir des résultats précis.
- Banquiers : les mathématiques financières sont au cœur du métier de banquiers, que ce soit le banquier en agence ou le banquier au siège. En effet, le banquier en agence devra comprendre toutes ces notions pour aiguiller ses clients et communiquer des informations précises. Les banquiers au siège seront plus focalisés sur les prêts proposés aux entreprises. Là encore, la maitrise des mathématiques financières est incontournable.



 Suivez-nous sur LinkedIn et Instagram pour plus de contenu et conseils :
Suivez-nous sur LinkedIn et Instagram pour plus de contenu et conseils :

