Maitriser la notion d’intérêts capitalisés (« compound interest » en anglais) est très important aussi bien dans votre vie privée que dans votre vie personnelle. En effet, c’est un concept financier que vous serez amenés à rencontrer aussi bien dans un cadre professionnel que dans un cadre personnel. Les intérêts capitalisés sont notamment abordés lorsqu’il est question de prêter ou d’emprunter une somme d’argent. Vous comprenez maintenant pourquoi il est intéressant pour vous de connaitre et de bien comprendre la notion d’intérêts capitalisés. Le problème, c’est que vous ne savez certainement pas par où commencer. Et c’est là que The Big Win intervient. Nous avons pris la décision de rédiger un article complet pour vous permettre de tout savoir sur la notion d’intérêts capitalisés. Tout au long de cet article, nous aborderons la définition des intérêts capitalisés mais également la formule pour les calculer ou encore des exemples concrets d’application. Nous essayerons également d’élargir un peu le sujet afin de vous apporter une vision plus globale. Par conséquent, nous écrirons quelques mots pour décrire la différence entre intérêts capitalisés et intérêts simples, la différence entre un prêt et un emprunt, les différentes situations où vous serez confrontés aux intérêts capitalisés. Nous clôturerons cet article en décrivant les différents parcours d’études supérieures où les étudiants seront confrontés aux intérêts capitalisés. En résumé, c’est vraiment grâce à cet article que vous disposerez de toutes les connaissances nécessaires pour maitriser la notion d’intérêts capitalisés de bout en bout.  

Intérêts capitalisés : définition

Commençons tout d’abord par définir ce qu’est un intérêt au sens large avant d’entrer dans le vif du sujet.

L’intérêt représente la somme d’argent qu’un prêteur souhaite recevoir en échange de l’argent qu’il prête à un emprunteur. C’est notamment le cas lorsqu’un établissement bancaire vous prête des fonds pour vous permettre de financer votre résidence principale. Dans ce contexte bien précis, vous serez dans l’obligation de rembourser le montant de la somme empruntée et, en plus, de payer des intérêts. En règle générale, les intérêts ne sont que le résultat d’un calcul qui consiste à appliquer un taux d’intérêts à une somme d’argent. A titre d’exemple, c’est le taux d’intérêts que vous négocierez directement avec votre banque et non un montant d’intérêts bien précis.

La définition d’un intérêt étant désormais maitrisée, nous pouvons poursuivre en indiquant à notre lecteur qu’il existe deux types d’intérêts : les intérêts capitalisés et les intérêts simples. Comme vous pouvez le pressentir, cet article portera quasi uniquement sur la notion d’intérêts capitalisés. Néanmoins, nous tacherons de vous proposer une brève introduction à la notion d’intérêts simples.

Les intérêts sont caractérisés comme étant « capitalisés » à partir du moment où la période de calcul de ces derniers est inférieure à la durée du prêt. Lorsque cette période de calcul est effectivement inférieure à la durée du prêt, cela veut dire que les intérêts seront calculés à plusieurs reprises lors de la durée du prêt. Pour être beaucoup plus précis, cela veut dire que les intérêts, à chaque période de calcul, sont ajoutés au montant prêté qui sert ensuite de nouvelle base de calcul pour les intérêts de la période suivante.

Quoi de mieux qu’un exemple concret pour bien comprendre le principe des intérêts capitalisés ? Nous supposons donc un prêt de 100€ dont le taux d’intérêts capitalisés est de 10%. Les intérêts de la première période de calcul s’élèvent à 10€ car nous multiplions simplement la valeur du prêt de 100€ par le taux d’intérêts de 10%. Pour le calcul des intérêts de la période suivante, nous ajoutons les 10€ au montant du principal de notre prêt, le portant ainsi à 110€. La seconde période de calcul porte le niveau des intérêts à hauteur de 11€ (110€ * 10% = 11€). Nous ajoutons, une nouvelle fois, le montant des intérêts au principal de notre prêt qui atteint désormais un montant de 121€. Comme vous pouvez l’anticiper, le montant des intérêts de cette troisième période de calcul sera égal à 12,1€ (121€ * 10% = 12,1€). Ces intérêts seront encore une fois capitalisés, ce qui portera le montant de notre prêt à 133,1€. Et ainsi de suite…  

C’est par le biais de cet exemple fictif que nous prenons conscience du fait que les intérêts produisent de nouveaux intérêts et c’est bien là toute la spécificité des intérêts capitalisés. Au passage, afin d’éviter toutes confusions, nous informons notre lecteur que intérêts capitalisés et intérêts composés sont des synonymes.

Formule et explications pour calculer les intérêts capitalisés

Au cours du chapitre précédent, nous avons démontré toute la méthode pour calculer les intérêts capitalisés pas à pas. Ici, nous abordons deux formules : la formule qui permet de calculer les intérêts capitalisés d’un seul coup et la formule qui permet d’isoler le montant d’intérêts capitalisés.

Valeur future = valeur actuelle * (1 + taux d’intérêts capitalisés) ^{durée du prêt}

Intérêts capitalisés = Valeur future – valeur actuelle

Nous décryptons rapidement les deux formules évoquées ci-dessus :

La valeur actuelle représente la valeur du prêt / de l’emprunt au départ, c’est-à-dire le montant demandé par un emprunteur à sa banque. Dans notre exemple précédent, la valeur actuelle est 100€.

La valeur future correspond au capital de départ auquel nous avons ajoutés tous les intérêts capitalisés, c’est-à-dire le montant que doit s’acquitter l’emprunteur auprès de sa banque à la fin de la durée de son prêt. Dans notre exemple précédent, la valeur future est 133,1€.

Afin de faciliter la compréhension de notre lecteur, nous allons appliquer ces formules à partir de l’exemple que nous avons évoqué dans le premier chapitre de cet article. Par conséquent, nous parlerons d’un prêt de 100€ avec un taux de 10%. Nous ajoutons une donnée supplémentaire : la durée du prêt qui est égale à 3 ans.

Par le biais de la formule ci-dessus, nous pouvons facilement vérifier que la valeur future de notre prêt est bien égale à 133,10€ :

Valeur future = 100€ * (1+10%)³ = 133,1€.

Grâce à la formule des intérêts capitalisés, nous pouvons isoler le montant global des intérêts capitalisés qui est égale à 33,1€.

Intérêts capitalisés = 133,1€ – 100€ = 33,1€.

En résumé, un particulier qui emprunte 100€ à la date d’aujourd’hui, devra restituer à sa banque, dans 3 ans, la somme de 133,1€. Dans cet exemple, l’établissement bancaire perçoit donc 33,1€ d’intérêts capitalisés pour avoir prêté 100€.

Quelle différence entre un prêt et un emprunt ?

A ce stade, la notion d’intérêts composés est certainement beaucoup plus claire dans votre esprit. Nous en profitons donc pour évoquer la différence qui subsiste entre un prêt et un emprunt. Ici, il n’y a absolument aucun piège dans la mesure où prêt et emprunt font référence à la même opération. En revanche, c’est le point de vue adopté qui change.

En effet, nous parlons de prêt à partir du moment où nous prêtons de l’argent à un emprunteur. Ainsi, c’est bien le prêteur qui perçoit les intérêts capitalisés liés au prêt d’argent qu’il accorde.

Par opposition, l’emprunt représente l’argent que nous demandons à un prêteur. Dans ce cas de figure, l’emprunteur doit s’acquitter des intérêts capitalisés lorsqu’il rembourse le prêteur.

Quel que soit le point de vue adopté, la notion d’intérêts capitalisés reste la même. Tout comme la méthode de calcul.

Les principales différences entre intérêts capitalisés et intérêts simples

Par définition, les intérêts capitalisés s’opposent aux intérêts simples. Les intérêts sont « simples » à partir du moment où la période de calcul des intérêts est proportionnelle à la durée du totale du prêt. Pour être plus explicite, les intérêts sont simples lorsqu’ils sont calculés qu’une seule fois sur toute la durée du prêt. Par conséquent, les intérêts ne sont payés qu’une seule fois, à la fin du prêt.

Par opposition, et comme nous l’avons déjà dit précédemment, les intérêts capitalisés se calculent plusieurs fois pendant la longévité du prêt ce qui permet aux intérêts de générer de nouveaux intérêts. C’est pour cela que nous disons qu’ils sont capitalisés et qu’ils s’opposent par nature aux intérêts simples.

Intérêts capitalisés : l’effet multiplicateur

Nos lecteurs les plus rusés auront remarqué qu’il existe un effet multiplicateur lorsqu’il est question d’intérêts capitalisés. Comme nous souhaitons que cet effet soit compris par tous, nous avons démontré, graphiquement, la différence entre les intérêts capitalisés et les intérêts simples calculés à partir du même capital de départ. Pour ce graphique, nous reprenons le même exemple que nous avons utilisé jusqu’à présent, à savoir un capital de 100€ et un taux d’intérêt de 10%. Le graphique représentera donc la valeur future de ce capital, année par année, sur une période de 10 ans. Une courbe sera consacrée aux intérêts capitalisés tandis que l’autre courbe sera consacrée aux intérêts simples.

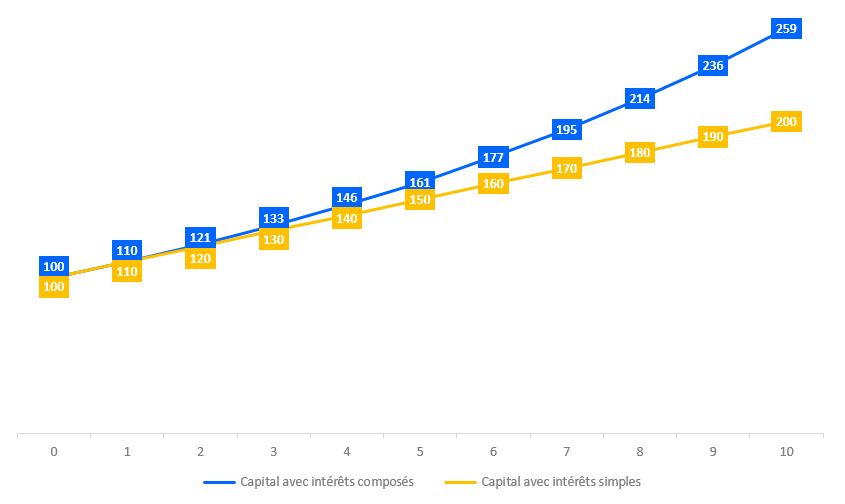
Comme vous pouvez le voir, le constant est frappant. Nous remarquons que plus nous avançons dans le temps et plus les deux courbes s’éloignent ce qui traduit bien une différence de valeur entre les intérêts simples et les intérêts composés.

Après une décennie, la différence qui existe entre le capital avec intérêts composés et le capital avec intérêts simples est saisissante. La valeur future du capital avec intérêts simples est 1,00 fois supérieure à la valeur actuelle du capital (200€ / 100€ – 1) tandis que la valeur future du capital avec intérêts composés est 1,59 fois supérieure à la valeur actuelle du capital (259€ / 100€ – 1).   

Nous communiquons, ci-dessous, les deux formules permettant d’obtenir ces résultats

Nous indiquons les deux formules permettant d’aboutir à ces résultats ci-dessous :

Capital avec intérêts capitalisés – période 10 = 100€ * (1 + 10%)¹⁰ = 259€

Capital avec intérêts simples – période 10 = 100€ * (1 + 10% * 10) = 200€

Inutile de préciser que cet effet multiplicateur illustre bien toute la force des intérêts capitalisés. Ce n’est d’ailleurs pas un hasard si certaines personnalités désormais mondialement connues ont délivré des citations célèbres sur la notion d’intérêts capitalisés. Pour les plus curieux, nous postons ci-dessous celles que nous trouvons les plus percutantes :

« My wealth has come from a combination of living in America, some lucky genes, and compound interest » – Warren Buffett

« Compound interest is the eighth wonder of the world. He who understands it earns it … he who doesn’t, pays it » – Albert Einstein

Qu’est-ce qu’un taux d’intérêt au sens large du terme ?

A ce stade de l’article, notre lecteur maitrise parfaitement la notion d’intérêts capitalisés. Il est donc temps pour nous d’étudier un peu plus en détails la notion de taux d’intérêts au sens large du terme. Car oui, un taux d’intérêt n’est pas simplement un pourcentage appliqué à un montant emprunté. La notion de taux d’intérêt est bien plus large que ça. Dans ce chapitre, nous essayons d’exposer différents axes de réflexions sur la définition et l’interprétation du taux d’intérêt.

• Tout d’abord, il faut bien avoir en tête que le taux d’intérêt représente la rémunération du prêteur. Un prêteur ne vous prêtera jamais de l’argent à titre gratuit. Tout simplement car il encourt un risque lorsqu’il prête son argent : le risque que l’emprunteur soit, un jour, dans l’incapacité de restituer l’argent prêtée. Il est donc normal pour le prêteur de se rémunérer sur l’argent qu’il prête à ses emprunteurs. D’une certaine manière, le prêt d’argent peut être perçu comme un service qui, logiquement, mérite rémunération. Sur notre exemple du premier chapitre, le prêteur a prêté 100€ et a été rémunéré à hauteur de 33,1€ pour avoir offert ce service à l’emprunteur.
• Dans la continuité du point précédent, le taux d’intérêt s’apparente également à la rentabilité espérée d’un prêteur. Nous pensons que ce point se différencie de la rémunération du prêteur en fonction de notre place dans le temps par rapport à l’opération en question. Toujours avec le même exemple que celui du chapitre 1, nous parlons de rémunération lorsque l’emprunteur aura effectivement payer les intérêts capitalisés de 33,1€. En revanche, lorsque emprunteur et prêteur négocient le contrat de prêt avant de le débuter, la rentabilité attendue du prêteur correspond au taux d’intérêt qu’il appliquera au capital qu’il prêtera à l’emprunteur, autrement dit le taux d’intérêt de 10%.
• Il faut aussi avoir en tête que risque et taux d’intérêt sont des notions étroitement liées. En effet, le risque qu’encours un prêteur lorsqu’il prête son argent influera grandement la rentabilité qu’il attendra et donc le taux d’intérêt qu’il sera susceptible d’appliquer. Même si le risque n’est pas l’unique composante pouvant faire fluctuer un taux d’intérêt, nous ne pouvons pas nier le fait qu’il existe bel et bien une trace de risque lorsque nous parlons de taux d’intérêt.

Les intérêts capitalisés dans la vie courante

Comme nous l’avons précisé en début d’article, les intérêts capitalisés sont réellement présents dans notre quotidien aussi bien professionnel que personnel. La notion d’intérêts capitalisés n’est pas un simple concept théorique financier, d’où l’importance de bien la maitriser. Il faut savoir que vous rencontrerez, tôt ou tard, cette notion dans votre vie courante aussi bien à votre échelle d’individu qu’à l’échelle de l’entreprise dans laquelle vous travaillerez.

Il nous semblait donc intéressant de vous citer des exemples concrets où les intérêts capitalisés sont appliqués et calculés. Nous avons donc regroupé plusieurs situations où vous serez confrontés aux intérêts capitalisés. La liste d’exemple que nous proposons ci-dessous est, bien évidemment, non exhaustive :

• Lors d’un emprunt à moyen – long terme, nécessaire pour financer l’acquisition d’un actif (exemple : prêt immobilier, prêt avec option d’achat d’un véhicule, crédit à la consommation, etc…) ;
• Lors d’un placement à moyen – long terme (exemple : obligations, comptes d’épargne, etc…).

Où retrouve-t-on la notion d’intérêts capitalisés dans les études en finance ?

Si vous envisagez de suivre un cursus en finance, nul doute que la notion d’intérêts capitalisés sera enseignée à un moment ou un autre. De manière générale, nous retrouvons les intérêts capitalisés dans la matière « mathématiques financières ». Sachez que, quel que soit votre orientation en finance (finance de marché ou finance d’entreprise), vous n’échapperez pas à cette matière. D’où l’importance de maitriser cette notion sur le bout des doigts pour réussir haut la main vos examens de mathématiques financières.

La question que vous avez certainement en tête : dans quel cursus la matière mathématiques financières est-elle enseignée ? Laissez-nous vous répondre que, globalement, nous retrouvons cette matière dans les cursus Post BAC + 3, aussi bien en école de commerce qu’en université. La subtilité à apporter ici est que la matière mathématiques financières sera proposée en tronc commun lors d’un cursus en école de commerce tandis qu’en université, la matière sera enseignée ou non en fonction de votre spécialisation. Il faut également savoir que nous retrouvons cette matière lors de certains cursus Post BAC +2 comme par exemple en classes préparatoires (exemple : voie technologique) ou encore dans certains DUT (exemple : le DUT GEA – Gestion des Entreprises et des Administrations).

Il nous semble également important de mentionner tous les cursus banque / assurance où la notion d’intérêts capitalisés sera forcément abordée. Notez que ce chapitre reste générique et que nous avons certainement oublié des formations et / ou des établissements scolaires où les mathématiques financières pourraient être introduites voire enseignées.