La notion d’intérêts composés (ou « compound interest » en anglais) est primordiale aussi bien dans votre future carrière de financier que dans votre vie personnelle. Il est donc très important de connaitre la notion d’intérêts capitalisés sur le bout des doigts (intérêts composés et intérêts capitalisés étant des synonymes). En effet, la notion d’intérêts composés est omniprésente lorsqu’il s’agit d’emprunter ou de prêter de l’argent. C’est donc tout naturellement que la notion d’intérêts composés peut aussi bien être présente dans votre futur quotidien de financier que dans votre vie personnelle. Si cette notion est encore floue pour vous, pas de panique ! La rédaction The Big Win s’est mobilisée pour vous préparer un article qui vous servira de guide pour tout comprendre sur les intérêts composés. C’est en lisant cet article que vous découvrirez à quoi correspondent réellement les intérêts composés mais aussi la formule pour les calculer ou encore des exemples concrets d’application. Notre but sera également d’élargir ce sujet afin de pouvoir évoquer la différence qui existe entre intérêts simples et intérêts composés, de déterminer la différence entre un prêt et un emprunt ou encore de mentionner les différentes situations où vous aurez affaire à des intérêts composés, aussi bien d’un point de vue personnel que professionnel. Vous l’aurez certainement compris, c’est grâce à cet article que la notion d’intérêts composés n’aura plus aucun secret pour vous !

Définition des intérêts composés

Avant d’entrer dans le vif du sujet, nous commençons par la base et nous donnons, dans un premier temps, la définition de l’intérêt.

Il faut savoir que l’intérêt correspond à la somme d’argent qu’un prêteur attend en échange de l’argent qu’il prête à un emprunteur. A titre d’exemple, lorsqu’une banque prête une certaine somme d’argent à un particulier pour le financement de son logement, elle attendra un intérêt en plus de l’argent qu’elle aura prêté. Dans cette situation, l’emprunteur doit donc restituer la somme prêtée et doit s’acquitter des intérêts appliqués. Pour déterminer le niveau des intérêts d’un prêt, il convient d’utiliser un taux d’intérêt. C’est ce taux d’intérêt que la banque appliquera à la somme empruntée pour déterminer le montant d’intérêts qu’elle attend en retour.  

Maintenant que les bases sont posées, nous pouvons élargir la notion d’intérêts en précisant qu’il existe deux types d’intérêts : les intérêts simples et les intérêts composés. Cet article sera principalement dédié à la notion d’intérêts composés même si nous n’oublierons pas de couvrir brièvement la notion d’intérêts simples un peu plus tard au cours de cet article.

Les intérêts se définissent comme étant « composés » dans la mesure où leur période de calcul est inférieure à la durée du prêt. Lorsque la période de calcul des intérêts est inférieure à la durée du prêt, cela signifie que les intérêts doivent être calculés plusieurs fois au cours de la durée du prêt. Pour être un peu plus explicite, les intérêts sont composés à partir du moment où, à chaque période de calcul, ils sont ajoutés au montant prêté qui sert ensuite de nouvelle base pour le calcul des intérêts de la période suivante.

Pour donner un exemple très simplifié, prenons l’exemple d’un prêt de 100€ dont le taux d’intérêt composé est de 10%. Sur la première période de calcul, les intérêts s’élèveront à 10€ (100€ * 10%). Ces 10€ seront ajoutés au montant du capital emprunté qui atteindra 110€. Par conséquent, le calcul des intérêts de la période suivante s’effectuera sur la somme de 110€. Sur la seconde période de calcul, les intérêts s’élèveront à 11€ (110€ * 10%). Nous ajoutons une nouvelle fois le montant de ces intérêts au capital qui contient déjà les intérêts de la période précédente. Pour le calcul des intérêts capitalisés de la troisième période, le capital s’élève à 121€ (100€ de capital de départ + 10€ d’intérêts de la période 1 + 11€ d’intérêts de la période 2). Sur cette troisième période, le montant des intérêts s’élève à 12,1€ (121€ * 10% = 12,1€). Ces 12,1€ seront ajoutés une nouvelle fois au capital, le portant ainsi à 133,1€ et ainsi de suite.  

Dans cet exemple, nous pouvons constater que les intérêts produisent de nouveaux intérêts et c’est bien là toute la particularité des intérêts capitalisés.

Le calcul des intérêts composés : formule et explications

Comme vous pouvez le constater, nous avons montré la manière dont les intérêts composés se calculaient, pas à pas. Dans cette partie, nous communiquons deux formules liées aux intérêts composés : la première formule permet de calculer le montant d’intérêts composés tandis que la seconde permet de calculer la valeur future de l’argent emprunté en tenant compte des intérêts composés.

Intérêts composés = Valeur future – valeur actuelle

Valeur future = valeur actuelle * (1 + taux d’intérêts composés) ^{durée du prêt}

Avant de vous proposer un exemple concret, il convient de décrypter certaines composantes des formules ci-dessus.

La valeur actuelle correspond au capital de départ, c’est-à-dire le montant qu’un emprunteur ira demander à sa banque.

La valeur future correspond au capital de départ additionné des intérêts capitalisés, c’est-à-dire le montant qu’un emprunteur aura restitué à sa banque à la fin de son prêt.

Afin de faciliter la compréhension des éléments ci-dessus, nous proposons l’exemple selon lequel un particulier emprunte 100€ à la banque. La banque accepte la demande d’emprunt et applique un taux de 10% et une durée de prêt égale à 5 ans.

La valeur future de ce prêt correspondra à 161,05€ que nous obtenons en appliquant la formule vue ci-dessus :

Valeur future = 100€ * (1+10%)⁵ = 161,05€.

Sur cette opération, le montant des intérêts composés s’élève à 61,05€ que nous obtenons en faisant la différence entre la valeur future et la valeur actuelle.

Intérêts composés = 161,05€ – 100€ = 61,05€.

En conclusion, ce particulier emprunte 100€ aujourd’hui et devra avoir remboursé 161,05€ au bout des cinq années d’emprunt en fonction d’un calendrier fixé par la banque. Dans cet exemple, la banque aura perçu 61,05€ d’intérêts composés pour avoir prêté seulement 100€.

Intérêts composés : prêt versus emprunt ?

Maintenant que vous êtes beaucoup plus familiers avec la notion d’intérêts composés, nous tenons à faire un aparté sur la différence entre un prêt et un emprunt. Il faut savoir que le prêt et l’emprunt font référence à la même opération. La seule différence réside dans le point de vue que nous adoptons.

Nous parlerons d’emprunt lorsque nous serons dans la peau d’un emprunteur qui demandera à ce qu’on lui prête de l’argent. Dans ce cadre, l’emprunteur devra payer des intérêts composés pour l’argent qu’il aura emprunté.

A l’inverse, nous parlerons de prêt lorsque nous serons dans la peau d’un prêteur qui répondra à la demande d’un emprunteur en lui prêtant de l’argent. Dans ce schéma, le prêteur recevra des intérêts composés pour l’argent qu’il aura prêté.

En tout état de cause, la notion d’intérêts composés reste identique quel que soit le point de vue (prêt ou emprunt). La méthode de calcul reste également identique.

Quelles différences entre les intérêts composés et les intérêts simples ?

Par nature, les intérêts capitalisés et les intérêts simples s’opposent. En effet, les intérêts sont « simples » à partir du moment où la période de calcul des intérêts est proportionnelle à la durée totale du prêt. En clair, les intérêts sont définis comme étant « simples » lorsqu’ils ne doivent être calculés qu’une seule fois durant toute la durée du prêt. En conséquence, les intérêts ne sont payés qu’une seule fois, à la fin de la durée du prêt.

A l’inverse, les intérêts composés sont calculés plusieurs fois pendant la durée du prêt et permettent donc de générer de nouveaux intérêts. C’est la raison pour laquelle nous disons qu’ils sont composés et qu’ils s’opposent aux intérêts simples. En clair, les intérêts capitalisés ont logiquement une période de calcul qui est inférieure à la durée totale du prêt, d’où la nécessité de les calculer plusieurs fois ce qui explique que nous devons les accumuler.

L’effet multiplicateur des intérêts composés

Nos lecteurs les plus avertis auront tout de suite compris que les intérêts composés jouissent d’un effet multiplicateur que les intérêts simples n’ont pas. Afin que cette subtilité soit bien comprise de tous, nous proposons le graphique ci-dessous où nous comparons la différence entre les intérêts capitalisés et les intérêts simples calculés sur le même capital de départ. Pour notre exemple, nous reprenons les bases de l’exemple que nous avons présenté ci-dessus, c’est-à-dire un capital de 100€, un taux d’intérêt de 10%. Pour accentuer l’effet multiplicateur que nous souhaitons observer, nous opterons pour une durée d’opération égale à 10 ans.

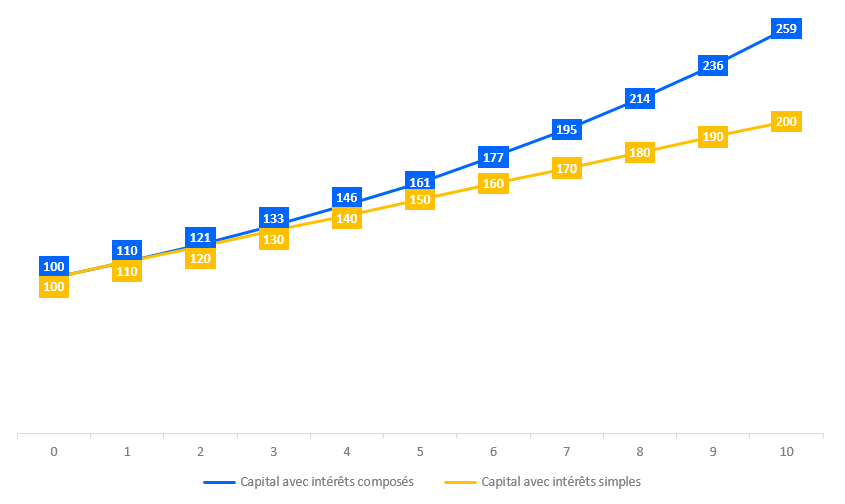
Le graphique ci-dessus représente l’évolution de la valeur future du capital après chaque période. La courbe bleue représente l’évolution de la valeur future en tenant compte des intérêts composés tandis que la courbe jaune représente l’évolution de la valeur future en tenant compte des intérêts simples. Le constant est frappant.

Au bout de 10 périodes, nous remarquons bien la différence qu’il y a entre le capital avec intérêts composés et le capital avec intérêts simples. En effet, le capital avec intérêts composés est 1,59 fois supérieur au capital de départ (259€ / 100€ – 1) tandis que le capital avec intérêts simples est seulement 1,00 fois supérieur au capital de départ (200€ / 100€ – 1).

Nous indiquons les deux formules permettant d’aboutir à ces résultats ci-dessous :

Capital avec intérêts composés – période 10 = 100€ * (1 + 10%)¹⁰ = 259,3742…€

Capital avec intérêts simples – période 10 = 100€ * (1 + 10% * 10) = 200€

Ici, l’effet multiplicateur est clairement identifiable et démontre bien toute la puissance des intérêts composés s’ils sont compris et maitrisés. D’ailleurs, les intérêts composés sont mondialement connus et ceux depuis très longtemps. Par le passé, de nombreuses personnalités ont eu l’occasion de mentionner les intérêts composés au travers de citations désormais mondialement connues. Nous retiendrons les deux suivantes :

« Compound interest is the eighth wonder of the world. He who understands it earns it … he who doesn’t, pays it » – Albert Einstein

« My wealth has come from a combination of living in America, some lucky genes, and compound interest » – Warren Buffett

Qu’est-ce qu’un taux d’intérêt au sens large du terme ?

Maintenant que notre lecteur est à l’aise avec cette notion, nous pouvons creuser un peu plus la notion de taux d’intérêt au sens large du terme. En effet, le taux d’intérêt est une notion importante qui ne se résume pas simplement à un pourcentage qui s’applique à une somme d’argent. Cette notion va bien au-delà de cette limite que nous tachons d’exposer dans cette partie. Nous avons donc regroupé ci-dessous quelques axes de réflexions portant sur la définition du taux d’intérêt au sens large du terme :

• Vous l’avez certainement compris mais nous souhaitons l’écrire noir sur blanc : le taux d’intérêt n’est autre que la rémunération du prêteur. Il serait naïf de croire qu’un prêteur accorde de l’argent à un emprunteur gratuitement. En effet, il est important de rappeler que le prêteur prend le risque de ne pas retrouver son argent en le prêtant à quelqu’un. Par conséquent, il se rémunère sur l’opération en appliquant un taux d’intérêt. En prenant l’exemple que nous présenté plus haut, le prêteur a pris le risque de prêter 100 euros en contrepartie de recevoir 61,05€ d’intérêts composés. En d’autres mots, sur cette opération, la rémunération du prêteur est de 61,05€.
• Par extension au point précédent, le taux d’intérêt peut aussi être perçu comme étant la rentabilité attendue par l’entité qui prête de l’argent. Ce point se différencie légèrement du point précédent en fonction du point de vue adopté. En reprenant l’exemple de cet article, lorsque le prêteur effectue son calcul d’intérêts composés et estime qu’il doit recevoir 61,05€ en échange de l’argent qu’il prête, il détermine la rentabilité qu’il espère de cette opération. En revanche, à la fin du prêt, lorsque l’emprunteur a restitué les 100€ et payé les 61,05€, nous pouvons dire que les 61,05€ d’intérêts composés représentent la rémunération du prêteur.
• Il ne faut aussi pas oublier que le taux d’intérêt traduit, d’une certaine manière, une forme de risque. Si le prêteur juge que prêter son argent est risqué, il sera certainement tenté d’appliquer un taux d’intérêt élevé pour atténuer le risque qu’il encourt. Il est évident que le risque n’est pas l’unique variable pouvant faire varier les taux d’intérêts pratiqués par les différents établissements prêteurs qui composent notre société. Néanmoins, il est important d’avoir en tête qu’il existe une « trace » de risque dans la notion de taux d’intérêt et que la situation financière de l’emprunteur jouera un rôle crucial dans sa capacité à rembourser ou non l’argent empruntée. 

Les intérêts composés dans la vie courante

Nous l’avons évoqué dans l’introduction de cet article et c’est ici que nous décidons d’en parler. Les intérêts composés font partie de notre quotidien aussi bien professionnel que personnel. En effet, la notion d’intérêts composés n’est pas simplement un concept théorique financier. Nous pouvons être amenés à rencontrer cette notion dans différentes situations de la vie courante aussi bien à l’échelle d’un individu qu’à l’échelle d’une entreprise.

Dans ce chapitre de l’article, nous avons jugé intéressant de présenter certains exemples concrets afin que notre lecteur puisse prendre conscience et réellement comprendre la notion d’intérêts composés. Vous trouverez donc, ci-dessous, une liste non exhaustive des différentes occasions où nous retrouvons des intérêts composés :

• Lors d’un emprunt à moyen – long terme, nécessaire pour financer l’acquisition d’un actif (exemples : prêt immobilier, prêt avec option d’achat d’un véhicule, crédit à la consommation, etc…) ;
• Lors d’un placement à moyen – long terme (exemple : obligations).

La notion d’intérêts capitalisés dans les études en finance

Si vous souhaitez faire carrière en finance, il faut savoir que la notion d’intérêts capitalisés sera forcément abordée, à un moment ou un autre, lors de votre cursus d’études supérieures. Les intérêts composés sont étudiés notamment dans la matière « Mathématiques financières ». Il est quasiment impossible d’échapper à cette matière lors d’un cursus en finance, et encore plus si vous êtes intéressés par la finance de marché. Celles et ceux qui pencheraient plutôt pour la finance d’entreprise, vous ne serez pas en reste non plus puisque cette matière sera également abordée. Il est donc primordial de maitriser le concept d’intérêts composés afin de réussir les différents examens qui animent la matière mathématiques financières.

Plus globalement, les mathématiques financières sont enseignées dans les cursus, après BAC + 3, en école de commerce et en universités. En école de commerce, la matière est étudiée lors des années de tronc commun tandis qu’en université, tout dépendra de votre spécialisation. Il est également possible de se frotter aux mathématiques financières lors de cursus BAC +2, notamment en classes préparatoires – voie technologique mais également dans certains DUT tel que le DUT GEA (Gestion des Entreprises et des Administrations).

Dans la volonté de proposer une vision globale de la matière, nous avons très certainement oublié certaines filiales où les mathématiques financières sont également abordées comme par exemple les cursus en banque et / ou en assurance.