Le CAPM (pour Capital Asset Pricing Model) est l’un des modèles mathématiques d’évaluation financière les plus célèbres qui existent, et de loin.
En effet, c’est un modèle utilisé par tous les fonds d’investissements, banques d’affaires, gérants et analystes buy-side ou sell-side. Autant vous dire qu’il touche un public très large et que pour faire carrière en finance vous devez le comprendre et savoir l’utiliser correctement.
Pas dinquiétude, The Big Win est là pour vous aider.

Modèle CAPM : définition et explication
La CAPM est un modèle mathématique financier qui fournit une approximation de la rentabilité attendue d’un actif financier, généralement une action.
CAPM est l’abréviation du nom anglais de ce modèle : Capital Asset Pricing Model, aussi parfois appelé en français le MEDAF pour Modèle d’Evaluation Des Actifs Financiers (terme que vous rencontrerez très peu cependant).
Ainsi, CAPM vous permet d’estimer quelle rentabilité (en pourcentage) attendre d’une action dans le futur en fonction de sa corrélation avec le marché.
Pour comprendre le principe du CAPM, il est nécessaire de comprendre un principe fondamental en finance : le rapport risque-rentabilité.
Ce principe stipule que plus un actif financier est risqué et plus la rentabilité potentielle qu’il doit apporter doit être élevée. Par conséquent, l’augmentation de la rentabilité est synonyme d’augmentation du risque et vice-versa.
En outre, on considère qu’il existe sur le marché, des actifs non risqués qui apportent une rentabilité faible pour un niveau de risque nul : c’est par exemple le cas des obligations d’Etats que l’on considère comme « sûrs » (Etats-Unis, Allemagne, Japon, France, Royaume-Uni, etc…). Ce taux est généralement appelé “Taux sans risque” ou “Risk free rate” en anglais.
Vous l’aurez compris, tout autre actif financier apporte une rentabilité plus élevée que le taux sans risque en échange d’un risque lui aussi plus élevé.
Or, c’est ce rapport risque-rentabilité qui est utilisé dans le modèle CAPM pour établir la rentabilité attendue d’un actif en fonction de son niveau de risque, tout simplement.
CAPM : la formule à connaitre et comprendre
Maintenant que vous avez compris le grand principe risque-rentabilité sur lequel est construit le modèle CAPM, voyons désormais sa formule :
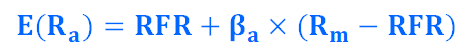
Avec :
- E(Ra) : la rentabilité attendue de l’actif a que nous souhaitons calculer
- RFR : le risk free rate, ou taux sans risque
- 𝛃a : le bêta de l’actif a
- Rm : la rentabilité moyenne du marché
Décryptons cette formule :
D’après le premier terme de la somme, RFR, la rentabilité attendue de notre actif sera au moins égale au taux sans risque RFR. Jusque-là c’est logique puisque que tout actif risqué doit apporter une rentabilité supérieure au taux sans risque d’après le principe risque-rentabilité vu précédemment.
Le terme suivant de la somme du CAPM fait apparaitre deux autres notions : le bêta 𝛃 et la rentabilité du marché Rm.
Commençons par le bêta : c’est la mesure de la corrélation entre la rentabilité de notre actif a et du marché m, c’est-à-dire la tendance d’évolution de notre actif par rapport à celle du marché :
- Plus le bêta est élevé, plus notre actif et le marché ont tendance à évoluer dans le même sens : lorsque le marché est haussier, notre actif a tendance à être haussier lui aussi.
- Plus le bêta est proche de 0, plus l’indépendance de l’actif par rapport au marché est élevée, c’est-à-dire que quelle que soit l’évolution du marché, on ne pourra pas l’utiliser pour prédire l’évolution de notre actif.
- Un bêta négatif signifie enfin que notre actif et le marché évoluent généralement dans des sens contraires : lorsque l’un est haussier, l’autre est baissier.
Le bêta est donc une mesure de risque de notre actif puisqu’il évalue la volatilité (les mouvements haussiers ou baissiers) de notre actif par rapport au marché.
La deuxième partie de ce terme est la différence entre la rentabilité du marché et le taux sans risque. C’est donc en quel que sorte la prime de risque lorsqu’on investit sur le marché par rapport à une rentabilité sans risque. C’est la prime de risque du marché.
Le produit du bêta, qui est une mesure de risque spécifique à notre actif par rapport au marché, multiplié par la prime de risque du marché nous donne donc une prime de risque pour notre actif.
Plus le bêta est élevé, plus notre actif est volatile (c’est-à-dire risqué) par rapport au marché, et plus ce produit (c’est-à-dire la prime de risque de notre actif) sera élevé. On respecte donc le principe de risque-rentabilité selon lequel plus de risque doit être compensé par plus de rentabilité.
Comme vous pouvez le voir, la formule du CAPM est parfaitement logique puisqu’elle met simplement en pratique le principe de risque rentabilité qui stipule qu’un actif risqué doit apporter une rentabilité au moins égale au taux sans risque plus une prime de risque.
Maintenant que nous avons vu la théorie, il convient de mettre en pratique ce concept avec un exemple concret. C’est justement l’objet de la partie suivante de notre article.
Exemple d’un calcul de CAPM avec l’action Apple
Prenons le cas de la célèbre entreprise Apple Inc, multinationale cotée au NASDAQ pour laquelle nous souhaitons calculer la rentabilité théorique attendue en fonction de son niveau de risque grâce au modèle CAPM. Nous prenons comme taux sans risque le taux du LIBOR. Au moment où nous écrivons cet article, le LIBOR 1 an cote à 1,7% (vous pouvez trouver les taux LIBOR sur Boursorama).
Pour calculer la prime de risque du marché, il nous faut la rentabilité moyenne du NASDAQ. Nous prenons la moyenne annualisée sur la plus grande durée possible afin d’avoir une donnée représentative. Au moment où nous rédigeons cet article, la rentabilité annuelle moyenne sur 15 ans du NASDAQ est de 12,9% (vous pouvez trouver cette information sur le site de Morningstar).
Enfin, pour le calcul de CAPM, il nous faut le bêta de l’entreprise. Deux solutions s’offrent généralement à vous :
- Soit le bêta est donné, c’est généralement le cas sur beaucoup de bases de données financières comme Yahoo finance ou Morningstar. Par exemple, sur la page Morningstar d’Apple, on peut voir qu’au moment où nous rédigeons cet article, le bêta d’Apple est de 1,21.
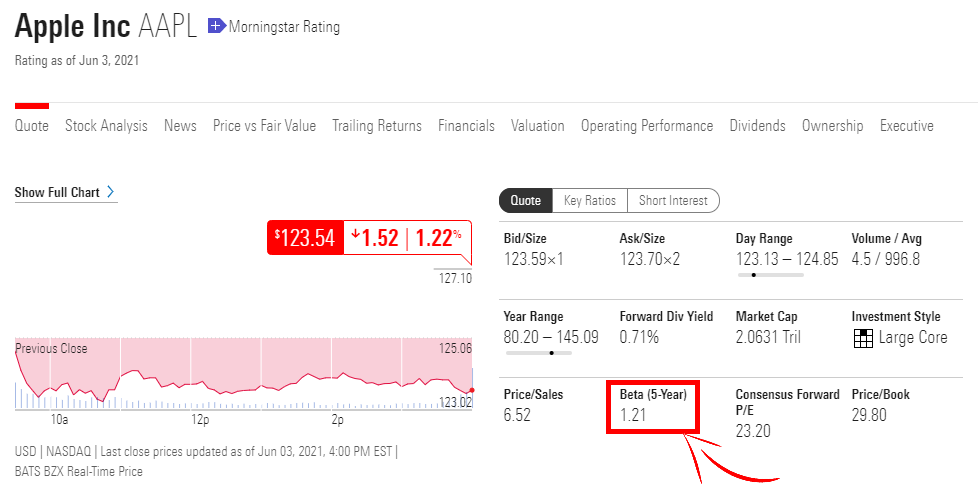
- Soit le bêta pour le calcul de CAPM n’est pas donné et dans ce cas il faut le calculer. La formule du bêta est la suivante : Bêta = Covariance (A,M) / Variance (A) où Covariance (A,M) est la covariance entre la rentabilité de l’actif A (ici Apple) et celle du marché M (ici le NASDAQ) et la Variance de la rentabilité A. La covariance et la variance sont des mesures statistiques calculées à partir d’espérances et d’écart-types. Vous pouvez trouver plus d’informations sur la covariance ICI et sur la variance ICI.
Maintenant que nous avons toutes les données nécessaires au modèle CAPM, nous pouvons calculer la rentabilité théorique attendue, notée E(Ra), d’une action Apple :
E(Ra) = 1,7% + 1,21 x (12,9% – 1,7%) = 15,25%
La rentabilité théorique annuelle attendue pour l’action Apple, étant donné le taux sans risque, la rentabilité du marché (le NASDAQ) et le rapport de risque entre le marché et l’action (représenté par le bêta) est de 15,25%.
L’utilisation du CAPM
Maintenant que nous savons calculer la rentabilité attendue d’une action (ou un autre type d’actif), voyons à quoi ce calcul peut nous servir.
Comparer la performance réelle et la performance attendue d’une action
La première utilisation clef d’un calcul de CAPM est de vérifier la performance réelle d’une action par rapport à la performance qui était attendue.
En effet, la rentabilité attendue obtenue avec le modèle CAPM est une rentabilité théorique, calculée à partir de données statistiques. Mais dans la réalité, cette action peut bien évidemment afficher une rentabilité différente de ce résultat de CAPM théorique. Voici les trois cas de figure possibles :
- La rentabilité réelle est supérieure à la rentabilité attendue théorique du modèle CAPM : on considère alors que l’action a surperformé puisque que sa rentabilité réelle a dépassé la rentabilité théorique qui était attendue. C’est donc un très bon investissement.
- La rentabilité réelle est égale à la rentabilité attendue théorique du modèle CAPM : on considère que l’action a performé normalement, ni trop, ni trop peu, puisqu’elle a atteint la rentabilité qui était attendue étant donné son niveau de risque (son bêta), la rentabilité de son marché et le taux sans risque. C’est un bon investissement, sans surprise.
- La rentabilité réelle est inférieure à la rentabilité attendue théorique du modèle CAPM : dans ce cas l’action a sous-performé. En effet, étant donné son niveau de risque (le bêta), le modèle CAPM nous a indiqué la rentabilité que devait offrir cette action et qu’elle n’a finalement pas réussi à atteindre. C’est donc un investissement considéré comme mauvais.
Si non reprenons notre exemple précédent de calcul de CAPM avec l’action Apple, le résultat était du modèle donnait une rentabilité théorique attendue de 15,25%. Or Morningstar nous indique aussi la rentabilité annualisée réelle d’Apple ces dernières années (disponible ici) :
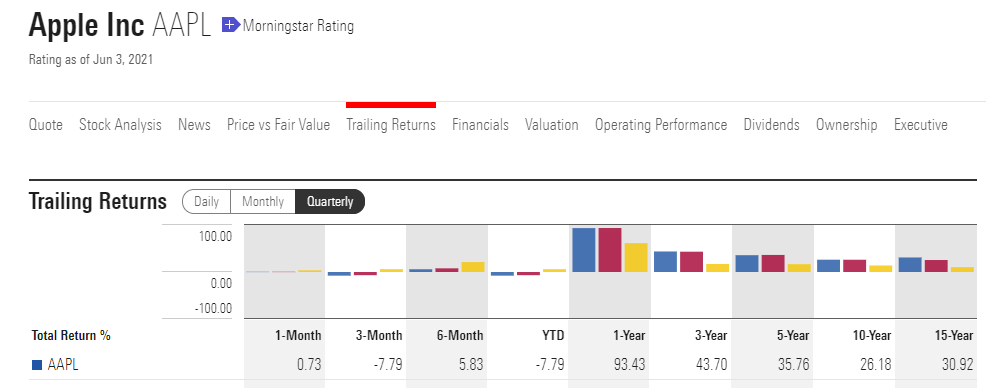
On remarque que sur les 15 dernières années, Apple a affiché une rentabilité annuelle moyenne de 30,92% (la dernière valeur du tableau), qui dépasse donc largement la rentabilité théorique calculée de 15,25% avec le CAPM.
On peut donc considérer que l’action d’Apple a surperformé sa rentabilité attendue (cela ne doit pas vous surprendre étant donné la réussite de l’entreprise à la pomme).
Faire un calcul de valorisation par les DCF
L’autre grande utilisation du CAPM est de calculer un taux de rendement pour une action afin de la valoriser avec un calcul de Discounted Cash Flow (DCF) ou de Gordon Growth.
En effet, le calcul de DCF vise à valoriser un actif en faisant la somme de ses cash flows futurs actualisés. Le principe qui sous-tend ce calcul est simplement de dire que la valeur d’un actif doit logiquement être égale à la valeur actuelle des revenus (les cash flows) que fournira cet actif dans le futur.
La formule des DCF est la suivante :
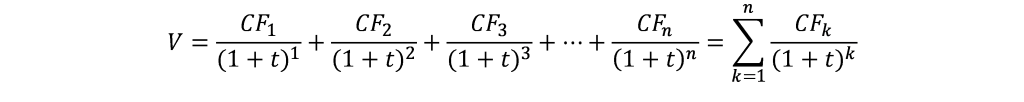
- V = la valorisation actuelle de l’actif que nous évaluons ;
- CF = cash flow de l’année 1, 2, 3, … n ;
- t = le taux d’actualisation que nous retenons.
La formule de Gordon Growth, que l’on peut utiliser pour valoriser un actif avec des cash flows perpétuels et un taux de croissance constant (par exemple une action de grande entreprise qui verse des dividendes) est la suivante :

- Vt = la valeur terminale de l’actif que vous étudiez
- CF = le cash flow que vous rapportera votre investissement “à l’infini”, par exemple, le dividende de votre action ou le loyer de votre appartement
- t = votre taux d’actualisation
- g = le taux de croissance des revenus de votre actif à l’infini si vous pensez que les revenus de votre investissement vont continuer d’augmenter “à l’infini”.
Nous avons d’ailleurs consacré un article dédié au calcul de DCF et de Gordon Growth accessible ici.
Or ces deux formules ont un point commun : ils nécessitent l’utilisation d’un taux d’actualisation t.
C’est justement ici qu’intervient le modèle CAPM car la rentabilité théorique attendu qu’il permet de calculer est bien souvent utilisée par les analystes financiers comme taux d’actualisation t.
Attention dans ce cas à ne pas faire d’erreur dans votre modèle CAPM. En effet, un calcul de valorisation par les DCF est très sensible au taux d’actualisation que l’on choisit. Il suffit que le taux d’actualisation change de quelques dixièmes de pourcents pour que le résultat de la valorisation évolue énormément.
Si vous utilisez le résultat de votre CAPM comme taux d’actualisation dans un calcul de DCF ou de Gordon Growth, vous devez donc faire attention de ne faire aucune erreur dans votre CAPM et d’utiliser des données (bêta, taux sans risque et rentabilité du marché) qui soient statistiquement représentatives de votre actif et calculées sur des durées assez longues pour éviter les biais statistiques.
Les limites du CAPM
Le modèle CAPM est donc extrêmement efficace et utile, notamment dans les métiers de gestion d’actifs et d’investissement. Pour autant, il ne faut pas le voir comme un outil infaillible et parfait : il comporte aussi certaines limites parmi lesquelles celles que nous vous listons ci-dessous :
Le choix des hypothèses
La première limite du CAPM est sa méthodologie de calcul elle-même. En effet, il dépend fortement des hypothèses que vous prendrez, en l’occurrence le taux sans risque, la rentabilité du marché et le bêta.
Tout d’abord, vous devez faire attention à prendre des données annualisées, notamment pour la rentabilité moyenne du marché. Concernant le taux sans risque, que vous choisissiez le LIBOR, l’EURIBOR ou une obligation d’Etat, choisissez un taux annuel pour rester cohérent.
D’ailleurs, le taux sans risque est le parfait exemple de la sensibilité du modèle CAPM au choix des hypothèses initiales. En effet, dans l’exemple précédent appliqué à l’action Apple, nous avons choisi un taux sans risque basé sur le LIBOR 1 an : 1,7%.
Si nous avions sélectionné une obligation du trésor américain (vous pouvez retrouver les taux souverains sur l’outil dédié de Boursorama), le taux aurait été de 0,2%. Dans ce cas, le calcul de CAPM et le résultat pour Apple auraient été les suivants : 0,2% + 1,2 x (12,9% – 0,2%) = 15,57%.
Si vous utilisez ensuite votre résultat de CAPM dans un modèle de Gordon Growth pour un calcul de valorisation, une telle différence peut avoir des impacts assez importants sur votre valeur finale.
Le CAPM a un caractère très théorique, parfois éloigné de la réalité de marché
La deuxième limitation du CAPM à laquelle il faut prêter beaucoup d’attention est son côté très théorique et parfois éloigné de la réalité des marchés financiers.
En effet, ce calcul est notamment basé sur la notion de bêta qui est une mesure purement statistique entre la rentabilité du marché et celle de l’action qui nous intéresse. Or les statistiques ont tendance à mal prévoir les évènements extrêmes tels que les crises financières.
De plus, étant un outil purement statistique, il ignore les aspects opérationnels de l’entreprise : le succès de ses produits, ses coûts, etc… ce que nous appelons en finance de marché les aspects d’analyse fondamentale d’une action ou d’une entreprise.
Retenez donc bien que le résultat du CAPM est uniquement un résultat théorique qui indique quelle rentabilité une action doit vous apporter pour justifier son niveau de risque, et en aucun cas une mesure fiable de ce que sera réellement sa rentabilité.
Notre exemple sur le calcul de CAPM de l’action Apple illustre d’ailleurs parfaitement cet aspect, puisque malgré un résultat de rentabilité théorique de 15,25%, la rentabilité réelle de l’action Apple sur ces 15 dernières années a atteint 30,92% en moyenne par an.



 Suivez-nous sur LinkedIn et Instagram pour plus de contenu et conseils :
Suivez-nous sur LinkedIn et Instagram pour plus de contenu et conseils :

